Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y = 2 cos x + 1 cos x - 2 . Khi đó ta có
A. 9M + m = 0
B. 9M - m = 0
C. M + 9m = 0
D. M + m = 0
Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 cos x + 1 cos x - 2 . Khi đó ta có:
A. 9M + m = 0
B. 9M - m = 0 .
C. M + 9m = 0
D. M + m = 0 .
Gọi M, m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2 cos x + 1 cos x - 2 . Khi đó ta có
A. 9M + m = 0 .
B. 9M - m = 0 .
C. M + 9m = 0 .
D. M + m = 0 .
Chọn: A
![]()
hàm số đã cho trở thành
![]()
Ta có:
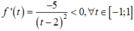
⇒ f t nghịch biến trên [-1; 1]
![]()
![]()
![]()
Gọi M, m tương ứng là giá trị lớn nhất và nhỏ nhất của hàm số y = sin x + 1 3 - 2 sin x . Khi đó ta có
A. M + 2019m = 2.
B. M - 2019m = -2019.
C. 2M + 3m = 0.
D. M + m = 1.
Chọn A
Đặt ![]() ta có
ta có ![]()
![]() với
với ![]() => hàm số đồng biến trên [-1;1]
=> hàm số đồng biến trên [-1;1]
![]()
![]()
Vậy M + 2019m = 2
Nên chọn A.
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = f(1-2cos x) trên 0 ; 3 π 2 . Giá trị của M + m bằng
A. 2
B. 1
C. 1 2
D. 3 2
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
Gọi M và m tương ứng là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = 2sin2x - cosx + 1 thì M.m bằng
A. 0
B. 25 8
C. 25 4
D. 2
Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = cos x + 2 . sin x + 3 2 . cos x - sin x + 4 . Tính M,m
A. 4/11
B. 3/4
C. 1/2
D. 20/11
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 2 là
A. m = - 1 2 ; M = 1
B. m = 1 ; M = 2
C. m = - 2 ; M = 1
D. m = - ; M = 2
Giá trị nhỏ nhất m và giá trị lớn nhất M của hàm số y = sin x + 2 cos x + 1 sin x + cos x + 2 là
![]()
![]()
![]()
![]()