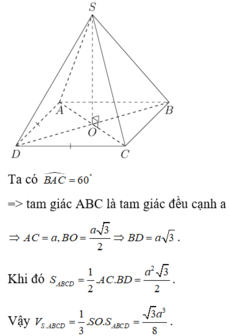
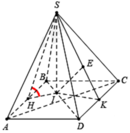
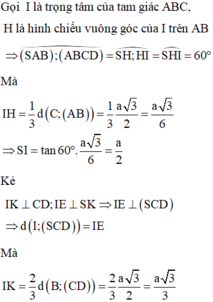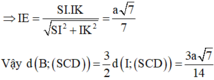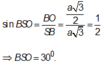Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và A B C ^ = 60 ° . Hình chiếu vuông góc của điểm S lên mặt phẳng A B C D trùng với trọng tâm tam giác ABC. Gọi φ là góc giữa đường thẳng SB với mặt phẳng S C D , tính sin φ biết rằng S B = a .
A. sin φ = 2 2
B. sin φ = 2 3
C. sin φ = 3 2
D. sin φ = 6 2