Cho f(x) có đạo hàm liên tục trên R và thỏa mãn f 2 = 16 , ∫ 0 1 f 2 x d x = 6 . Tính I = ∫ 0 2 x . f ' x dx ta được kết quả
A. I = 14
B. I = 20
C. I = 10
D. I = 4
Cho hàm số y=f(x) có đạo hàm liên tục trên R thỏa mãn x f x . f ' x = f 2 x - x , ∀ x ∈ R và f(2)=1 Tích phân ∫ 0 2 f 2 x d x bằng
A. 3 2
B. 4 3
C. 2
D. 4
Cho hàm số y=f(x) liên tục và có đạo hàm trên R thỏa mãn f(2)=-2, ∫ 0 2 f x d x = 1. Tính tích phân I = ∫ 0 4 f ' x d x .
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Cho hàm số y=f(x) có đạo hàm liên tục trên R thỏa mãn x f ( x ) . f ' ( x ) = f 2 ( x ) - x , ∀ x ∈ ℝ và f(2)=1 .Tích phân bằng
A. 3 2
B. 4 3
C. 2
D. 4
Chọn đáp án C.
Lấy tích phân hai vế trên đoạn [0;2] có
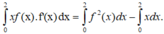
Tích phân từng phần có
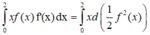
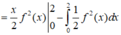
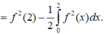
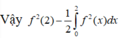
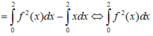
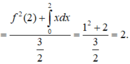
Cho hàm số y =f(x) liên tục và có đạo hàm trên R thỏa mãn f(2) = -2; ∫ 0 2 f ( x ) d x = 1 Tính tích phân ∫ 0 4 f ' ( x ) d x
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Cho hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn f(0) = 3 và f x + f 2 - x = x 2 - 2 x + 2 . Tích phân ∫ 0 2 x f ' x d x bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]()
Cho hàm số y = f(x) liên tục và có đạo hàm trên R thỏa mãn f(2) = -2; ∫ 0 2 f ( x ) d x = 1 Tính tích phân I = ∫ 0 4 f ' ( x ) d x
A. I = -10
B. I = -5
C. I = 0
D. I = -18
Cho hàm số f(x) có đạo hàm liên tục trên tập hợp R thỏa mãn ∫ 1 2 f 3 x - 6 d x = 3 và f(-3)= 2. Giá trị của ∫ - 3 0 x . f ' x d x bằng
A. -3
B. 11
C. 6
D. 9
Cho hàm số f(x) và g(x) liên tục, có đạo hàm trên R và thỏa mãn f ' 0 . f ' 2 ≠ 0 và g x f ' x = x x - 2 e x . Tìm giá trị của tích phân I = ∫ 0 2 f x g ' x d x
A. -4
B. e - 2
C. 4
D. 2 - e
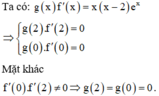
Áp dụng công thức tích phân từng phần ta có:
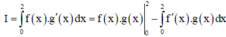
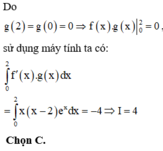
Xét hàm số f(x) có đạo hàm liên tục trên R và thỏa mãn điều kiện f(1)=1 và f(2)=4.
Tính J = ∫ 1 2 f ' ( x ) + 2 x - f ( x ) + 1 x 2 d x
A. J = 1 + ln 4
B. J = 4 - ln 2
C. J = ln 2 - 1 2
D. J = 1 2 + ln 4