Cho dãy tỉ số bằng nhau và .
Tính ta được
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Dựa vào các tính chất của dãy tỉ số bằng nhau , tìm a,b,c trong dãy tỉ số sau :
3X = 2Y ; 7Y = 6Z và X + 3Y - 2Z=12
Giải thích cách giải ( nếu được ) và giải bài này ( có thể nâng lên hạ xuống số )
Gíá trị tuyệt đối của một số hữu tỉ ; Hiểu và vận dụng được các tính chất của tỉ lệ thức, của Các phép tính cộng, trừ, nhân, chia,và lũy thừa thực hiện trong tập hợp số hữu tỉ; dãy tỉ số bằng nhau; khái niệm về số thực và căn bậc hai.
Hai góc đối đỉnh, hai đường thẳng vuông góc và hai đường thẳng song song, từ vuông góc đến song song.
giúp mik vs
Cho mình hỏi một tí : nếu như trong phần tính chất của dãy tỉ số bằng nhau ta có thể cho phép nhân đc ko ạ mọi ngừi !
VD như cái này ạ : Áp dụng tính chất của dãy tỉ số bằng nhau có : \(\frac{a}{1}=\frac{b}{4}=\frac{c}{9}=\frac{a.b.c}{1.4.9}=\frac{a.b.c}{36}\)
Mong mọi người chung tay giúp đỡ Phưn ạ!
cho mình hỏi : tính chất của tỉ lệ thức , dãy tỉ số bằng nhau
t/c tỉ lệ thức:Nếu thì a.d = b.c
Tính chất
Từ dãy tỉ số bằng nhau ab=cd=efab=cd=ef ta suy ra:
t/c dãy tỉ số = nhau:Mờ rộng
ab=cd=ef=a+c+eb+d+f=a−c+eb−d+fab=cd=ef=a+c+eb+d+f=a−c+eb−d+f
T/c của tỉ lệ thức:
1.Nếu a/b=c/d =>a.d=b.c
2.Nếu a.d=b.c và a,b,c,d khác 0
=> a/b=c/d ;a/c=b/d ;d/b=c/a ;d/c=b/a
T/c của dãy tỉ số = nhau :
Nếu có a/b=c/d=e/f thì a/b=c/d=e/f=(a+b+c)/(b+d+f)=(a-c-e)/(b-d-f)=(a-c+e)/(b-d+f)=(a-c)/(b-d)=(c-e)/d-f)=...v.v
k mk nha mấy bn nếu thấy đúng hì......
Tính chất của tỉ lệ thức là: Thuận :nếu \(\frac{a}{b}\)=\(\frac{c}{d}\)thì ad=bc
Đảo:nếu ad=bc thì :\(\frac{a}{b}\)=\(\frac{c}{d}\);\(\frac{b}{a}\)=\(\frac{d}{c}\);\(\frac{a}{c}\)=\(\frac{b}{d}\);\(\frac{c}{a}\)=\(\frac{d}{b}\)ai cho mình 1 bài toán hsg về chứng minh dãy tỉ số bằng nhau và lời giải được không
Hoạt động 5
Xét số vô tỉ: \(\sqrt 2 = 1,4142135624...\). Xét dãy số hữu tỉ: \({r_1} = 1;{r_2} = 1,4;{r_3} = 1,41;{r_4} = 1,414;{r_5} = 1,4142;{r_6} = 1,41421;...\) và \(\lim {r_n} = \sqrt 2 \). Bằng cách tính \({3^{{r_n}}}\) tương ứng, ta nhận được Bảng 1 ghi các dãy số \(\left( {{r_n}} \right)\) và \(\left( {{3^{{r_n}}}} \right)\) với n = 1, 2, …, 6. Người ta chứng minh được rằng khi \(n \to + \infty \) thì dãy số \(\left( {{3^{{r_n}}}} \right)\) dần đến một giới hạn mà ta gọi là \({3^{\sqrt 2 }}\). Nêu dự đoán về giá trị của số \({3^{\sqrt 2 }}\) (đến hàng phần trăm).
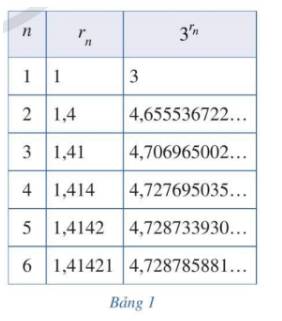
Từ hàng thứ 5 trở đi, số \(3^{r_n}\) càng gần với giá trị 4,728... Làm tròn đến hàng phần trăm, ta được \(3^{\sqrt{2}}\approx4,73\).
Cho dãy tỉ số bằng nhau: x/y=z/t=u/v(giả sử các tỉ số đã cho đều có nghĩa) suy ra được
tính chất dãy tỉ số bằng nhau: 2x=3y=5z và x+2y+z=41
\(2x=3y=5z\Leftrightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{15}=\frac{y}{10}=\frac{z}{6}=\frac{x+2y+z}{15+2.10+6}=\frac{41}{41}=1\)
\(\Leftrightarrow\hept{\begin{cases}x=1.15=15\\y=1.10=10\\z=1.6=6\end{cases}}\)
Cho em hỏi tính chất của dãy tỉ số bằng nhau
Cho tỉ lệ thức 2 phần 4 =3 phần 6
ta có : \(\frac{2}{4}\)= \(\frac{3}{6}\)\(\Rightarrow\)\(\frac{2}{4}\)= \(\frac{3}{6}\)= \(\frac{2+3}{4+6}\)= \(\frac{1}{2}\)
- HT -
x/y=3/4 và 2x+5y=-78 (áp dụng tính chất dãy tỉ số bằng nhau)
Ta có:4x=-7y ⇒⇒x−7=y4x−7=y4⇒⇒2x−14=3y122x−14=3y12
Theo tính chất của dãy tỉ số bằng nhau ta có:
2x−14=3y12=2x−3y−14−12=−78−26=32x−14=3y12=2x−3y−14−12=−78−26=3
2x−14=3⇒2x=3×(−14)=−42⇒x=−42÷2=−212x−14=3⇒2x=3×(−14)=−42⇒x=−42÷2=−21
3y12=3⇒3y=12×3=36⇒y=36÷3=123y12=3⇒3y=12×3=36⇒y=36÷3=12
Vậy x=-21,y=12
Từ \(\frac{x}{y}=\frac{3}{4}\)\(\Rightarrow\)\(\frac{x}{3}=\frac{y}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{2x}{6}=\frac{5y}{20}=\frac{2x+5y}{6+20}=\frac{-78}{26}=-3\)
\(\Rightarrow\hept{\begin{cases}\frac{x}{3}=-3\\\frac{y}{4}=-3\end{cases}}\)\(\Rightarrow\hept{\begin{cases}x=-9\\y=-12\end{cases}}\)
câu hỏi đi bạn