Trong không gian với hệ tọa độ Oxyz, cho ba điểm A − 3 ; 4 ; 2 , B − 5 ; 6 ; 2 , C − 4 ; 7 ; − 1 . Tìm tọa độ điểm D thỏa mãn AD → = 2 AB → + 3 AC → .
A. 10 ; − 17 ; − 7
B. − 10 ; − 17 ; − 7
C. 10 ; 17 ; 7
D. − 10 ; 17 ; − 7
PB
Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;3), B(0;2;1), C(-2;0;-3). Điểm M thuộc Oz sao cho
2
M
A
→
+
M
B
→
+
M
C
→
nhỏ nh...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;1;3), B(0;2;1), C(-2;0;-3). Điểm M thuộc Oz sao cho 2 M A → + M B → + M C → nhỏ nhất có tọa độ là:
A. (0;0;2)
B. (0;0;-1)
C. (0;0;1)
D. 0 ; 0 ; 1 2
Đáp án C.
Do M ∈ O z ⇒ M 0 ; 0 ; a ⇒ M A → = 1 ; 1 ; 3 - a , M B → = 0 ; 2 ; 1 - a , M C → = - 2 ; 0 ; - 3 - a
⇒ 2 M A → + M B → + M C → = 0 ; 4 ; - 4 a + 4 ⇒ 2 M A → + M B → + M C → = 4 a - 1 2 + 1 ≥ 4 xảy ra khi a = 1.
Do đó tọa độ điểm M là M(0;0;1).
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz , cho ba điểm . Tìm tọa độ điểm D thỏa mãn
A
D
→
2
A
B
→
+
3
A
C
→
A. (−10;−17;−7) B. (10;−17;−7) C. (10;17;7) D. (−10;17;−7 )
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz , cho ba điểm . Tìm tọa độ điểm D thỏa mãn A D → = 2 A B → + 3 A C →
A. (−10;−17;−7)
B. (10;−17;−7)
C. (10;17;7)
D. (−10;17;−7 )
Trong không gian với hệ tọa độ Oxyz , cho ba điểm
A
-
3
;
4
;
2
,
B
-
5
;
6
;
2
,
C
-
4
;
7
;...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz , cho ba điểm A - 3 ; 4 ; 2 , B - 5 ; 6 ; 2 , C - 4 ; 7 ; - 1 . Tìm tọa độ điểm D thỏa mãn A D → = 2 A B → + 3 A C →
A. (-10;-17;-7)
B. (10;-17;-7)
C. (10;17;7)
D. (-10;17;-7)
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(2;0;1), C(3;-1;5). Diện tích tam giác ABC là:
A. 3 2
B. 7 2
C. 5 2
D. 9 2
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(2;0;1), C(3;-1;5). Diện tích tam giác ABC là:
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(1;-2;3), B(2;0;1), C(3;-1;5). Diện tích tam giác ABC là:
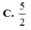
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm A(0; 0; 2), B(3; 0; 5), C(1; 1; 0). Tọa độ của điểm D sao cho ABCD là hình bình hành là
A. D(4; 1; 3)
B. D(-4; -1; -3)
C. D(2; 1; -3)
D. D(-2; 1; -3)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;3;5), B(2;0;1), C(0;9;0) Tọa độ trọng tâm G của tam giác ABC là
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho ba điểm A(1;3;5), B(2;0;1), C(0;9;0) Tọa độ trọng tâm G của tam giác ABC là
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho
M
A
→
+
M
B
→
+
M
C
→
có g...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho ba điểm A(2;-3;7), B(0;4;-3), C(4;2;5). Tìm tọa độ điểm M trên mặt phẳng (Oxy) sao cho M A → + M B → + M C → có giá trị nhỏ nhất
A. M(-2;-1;0)
B. M(-2;-1;0)
C. M(2;-1;0)
D. M(2;1;0)
Trong không gian với hệ tọa độ Oxyz cho ba điểm A (3;-2;4), B (5; 3;-2), C (0;4;2), đường thẳng d cách đều ba điểm A, B, C có phương trình là:
A
.
x
8
3
+
26
t
y
5...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho ba điểm A (3;-2;4), B (5; 3;-2), C (0;4;2), đường thẳng d cách đều ba điểm A, B, C có phương trình là:
A . x = 8 3 + 26 t y = 5 3 + 22 t z = 4 3 + 27 t
B . x = 4 + 26 t y = 2 + 22 t z = 9 4 + 27 t
C . x = 11 6 y = 1 6 + 22 t z = 27 t
D . x = 4 + 26 t y = 2 + 38 t z = 9 4 + 27 t
Chọn B
Gọi I là trung điểm của AB suy ra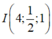 
và (P) là mặt phẳng trung trực của đoạn AB.
Mặt phẳng (P) đi qua I và nhận 
làm vec tơ pháp tuyến có phương trình là:
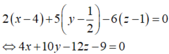
Gọi J là trung điểm của AC suy ra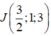 
và (Q) là mặt phẳng trung trực của đoạn AC
Mặt phẳng (Q) đi qua J và nhận 
làm vec tơ pháp tuyến có phương trình là:
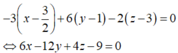
Khi đó d = (P) ∩ (Q)
Ta có d có vectơ chỉ phương 
và đi qua M là nghiệm của hệ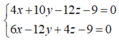 
, ta chọn x = 4 suy ra y = 2 và z = 9/4. Vậy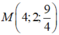 
Phương trình tham số của d là: 
Đúng 0
Bình luận (0)