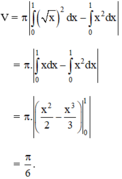Cho khối cầu có thể tích bằng 8 π a 3 6 27 , khi đó bán kính R của mặt cầu là:
A. R = a 2 3
B. R = a 6 2
C. R = a 3 3
D. R = a 6 3
Cho khối cầu có diện tích S=8 π , thể tích V của khối cầu bằng:
![]()
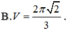
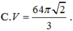
![]()
Cho hình cầu có diện tích mặt cầu là 64 π ( c m 2 ). Tính thể tích khối cầu?
A. 256 π 3 c m 3
B. 256 π c m 3
C. 64 π 3 c m 3
D. Đáp án khác
Cho khối trụ có bán kính đáy bằng a và thiết diện đi qua là một hình vuông. Thể tích khối trụ là:
A. 2 π a 3 B. 2 π a 3 /3
C. 4 π a 3 D. π a 3
Chọn A.
Thiết diện qua trục của hình trụ là hình vuông nê hình trụ có bán kính đáy là a, chiều cao là 2a.
Do đó thể tích khối trụ là:
V = πR 2 h = 2 πa 3
Một khối nón có diện tích toàn phần bằng 10 π và diện tích xung quanh bằng 6 π . Tính thể tích V của khối nón đó được:
![]()
![]()
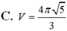
![]()
Quay hình phẳng Q giới hạn bởi các đường: y 1 = sinx và y 2 = 2x/ π quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích khối tròn xoay này bằng:
A. 1/6 B. π /6
C. 8 D. π 2 /6
Đáp án: D.
Vì thể tích khối này được tính bởi
![]()
như vậy A và C dễ thấy là sai.
Quay hình phẳng Q giới hạn bởi các đường: y 1 = sinx và y 2 = 2x/π quanh trục Ox, ta được một khối tròn xoay. Khi đó, thể tích khối tròn xoay này bằng:
A. 1/6 B. π/6
C. 8 D. π 2 /6
Đáp án: D.
Vì thể tích khối này được tính bởi
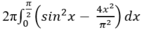
Một khối trụ có chu vi đáy bằng 6 π cm và thiết diện đi qua là một hình chữ nhật có độ dài đường chéo bằng 10 cm. Thể tích khối trụ là:
A. 72 π ( cm 3 ) B. 24 π ( cm 3 )
C. 48 π ( cm 3 ) D. 18 π 34 ( cm 3 )
Chọn A.
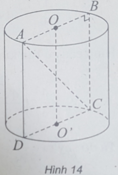
(h.14) Gọi O, O' là hai tâm của hai đáy hình trụ và thiết diện qua trục là hình chữ nhật ABCD.
Do chu vi đáy của hình trụ đó bằng 6 π (cm) nên bán kính đáy của hình trụ là: R = 3 (cm)
Vì thiết diện đi qua trục là một hình chữ nhật ABCD có AC = 10 (cm) và AB = 2R = 6 (cm) nên chiều cao của hình trụ là:
h = OO' = BC = 8 (cm)
Vậy thể tích khối trụ là: V = π R 2 h = 72 π ( cm 3 )
Cho mặt cầu (S) có bán kính R = 5 (cm). Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là đường tròn (C) có chu vi bằng 8 π (cm). Bốn điểm A, B, C, D thay đổi sao cho A, B, C thuộc đường tròn (C), điểm D thuộc (S) (D không thuộc đường tròn (C)) và tam giác ABC là tam giác đều. Thể tích lớn nhất của khối tự diện ABCD bằng bao nhiêu?
A. 32 3 ( c m 3 )
B. 60 3 ( c m 3 )
C. 20 3 ( c m 3 )
D. 96 3 ( c m 3 )
Cho mặt cầu (S) tâm O và các điểm A, B, C nằm trên mặt cầu (S) sao cho AB = AC = 6, BC = 8. Khoảng cách từ O đến mặt phẳng (ABC) bằng 2. Thể tích khối cầu (S) bằng
A. 404 π 5
B. 2916 π 5 75 .
C. 404 π 505 75
D. 324 π 5
Cho hình phẳng giới hạn bởi các đường y=√x và y=x quay xung quanh trục Ox. Thể tích của khối tròn xoay tạo thành bằng:
(A). 0
(B). –π
(C). π
(D). π/6
Chọn đáp án D.
Hoành độ giao điểm hai đồ thị là nghiệm của phương trình:
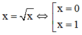
Thể tích cần tính: