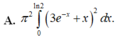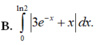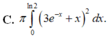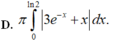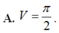
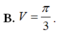
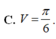
Cho hình phẳng D giới hạn bởi đường cong y = ln x , trục hoành và đường thẳng x=e. Tính thể tích V của khối tròn xoay tạo thành khi quay D quanh trục hoành.
A. 
.
B. 
.
C. 
.
D. 
.
Cho hình phẳng (H) giới hạn bởi đường cong y = ln x ,trục hoành, đường thẳng x=1và x=k (k>1) Gọi V k là thể tích khối tròn xoay thu được khi quay hình (H) quay quanh trục Ox. Biết rằng V k = π . Hãy chọn khẳng định đúng?
A. 3 < k < 4.
B. 1 < k < 2.
C. 2 < k < 3.
D. 4 < k < 5.
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x), y=0, x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0, x=a bằng:
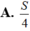
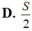
Biết diện tích hình phẳng giới hạn bởi đường cong y=f(x),y=0,x=0,x=2a bằng S. Diện tích hình phẳng giới hạn bởi đường cong y=f(2x), trục hoành Ox và hai đường thẳng x=0,x=a bằng
A. S/4.
B. 4S.
C. 2S.
D. S/2.
Cho (H) là hình phẳng giới hạn bởi đường cong y = x , trục hoành và đường thẳng y=2-x (phần tô đậm trong hình vẽ bên). Diện tích của (H) bằng
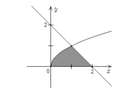
A. 4 2 - 1 3
B. 7 6
C. 8 2 + 3 6
D. 5 6
Cho hình phẳng (H) giới hạn bởi đường cong y = ln x x , trục hoành và đường thẳng x = e. Khối tròn xoay tạo thành khi quay (H) quanh trục hoành có thể tích V bằng bao nhiêu?
A. V = π 2
B. V = π 3
C. V = π 6
D. V = π
Đáp án B
Thể tích khối tròn xoay cần tính là V = π ∫ 1 e f 2 x d x = π ∫ 1 e ln 2 x x d x
Đặt t = ln x ⇔ d t = d x x và x = 1 ⇒ t = 0 x = e ⇒ t = 1 . Khi đó ∫ 1 e ln 2 x x d x = ∫ 0 1 t 2 d t = t 3 3 0 1 = 1 3 . Vậy V = π 3
Diện tích hình phẳng (H) giới hạn bởi đường cong bậc ba y = x 2 ( x - 6 ) và trục hoành bằng
A. 108.
B. 216.
C. 72.
D. 144.
Cho hình phẳng (H) giới hạn bởi đường cong y = 3 e − x + x , trục hoành và hai đường thẳng x = 0 , x = ln 2 . Thể tích khối tròn xoay tạo thành khi cho (H) quay quanh trục hoành được tính bằng công thức nào sau đây?
A. π 2 ∫ 0 ln 2 3 e − x + x 2 d x .
B. ∫ 0 ln 2 3 e − x + x d x .
C. π ∫ 0 ln 2 3 e − x + x 2 d x .
D. π ∫ 0 ln 2 3 e − x + x d x .
Đáp án C.
Chú ý rằng nếu hàm số y = f x liên tục trên a ; b , thể tích hình (H) tạo thành khi quay phần giới hạn bởi đồ thị hàm số y = f x , đường thẳng x = a và x = b quanh trục hoành là V = π ∫ a b f 2 x d x .
Cho hình phẳng (H) giới hạn bởi đường cong y = 3 e - x + x , trục hoành và hai đường thẳng x = 0 và x = ln2 . Thể tích khối tròn xoay tạo thành khi cho (H) quay quanh trục hoành được tính bằng công thức nào sau đây?
