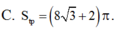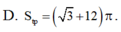Hình nón có đường sinh l=2a và hợp với đáy góc α = 60 0 . Diện tích toàn phần của hình nóng bằng
A. 4 π a 2
B. 3 π a 2
C. 2 π a 2
D. π a 2
Đáp án B
Hình nón có đường sinh l=2a và hợp với đáy góc 60 0 bán kính đáy là r = a
Vậy diện tích toàn phần cần tính là S = π r l + π r 2 = π . a .2 a + π a 2 = 3 π a 2
Cho hình trụ (T) có hai hình tròn đáy là (O) và (O'). Xét hình nón (N) có đỉnh O', đáy là hình tròn (O) và đường sinh hợp với đáy một góc α . Biết tỉ số giữa diện tích xung quanh hình trụ (T) và diện tích xung quanh hình nón (N) bằng 3 . Tính số đo góc α .
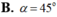
Cho hình trụ trục OO', đường tròn đáy (C) và (C'). Xét hình nón đỉnh O', đáy (C) có đường sinh hợp với đáy góc α ( 0 ∘ < α 90 ∘ ) . Cho biết tỉ số diện tích xung quanh của hình lăng trụ và hình nón bằng 3 . Tính giá trị α .
A. 30 ∘ .
A. 45 ∘ .
C. 60 ∘ .
A. Kết quả khác
Cho hình nón có bán kính đáy bằng 2a và độ dài đường sinh l = 5 a 2 . Diện tích toàn phần của hình nón bằng
A. 10 πa 2
B. 11 πa 2
C. 3 πa 2
D. 9 πa 2
Đáp án D
S t p = S x q + S d a y = π . R . l + π . R 2 = π 5 a 2 + 4 a 2 = 9 πa 2
Cho hình nón có bán kính đáy bằng 2a và độ dài đường sinh l= 5 a 2 Diện tích toàn phần của hình nón bằng
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Gọi I là một điểm trên đường cao DO của hình nón sao cho DI DO = k (0 < k < 1) . Tính diện tích thiết diện qua I và vuông góc với trục của hình nón.
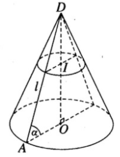
Thiết diện qua I và vuông góc với trục hình nón là một hình tròn bán kính r’
với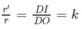 
Gọi s là diện tích của thiết diện và S là diện tích của đáy hình tròn ta có:
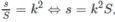
trong đó S = πr 2 = πl 2 cos 2 α
Vậy diện tích của thiết diện đi qua điểm I và vuông góc với trục hình nón là: s = k 2 s = k 2 πl 2 cos 2 α
Một hình nón tròn xoay có đỉnh là D, tâm của đường tròn đáy là O, đường sinh bằng l và có góc giữa đường sinh và mặt phẳng đáy bằng α . Tính diện tích xung quanh của hình nón và thể tích khối nón được tạo nên.
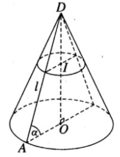
Gọi r là bán kính của đường tròn đáy.
Ta có OA = r = l.cos α (với O là tâm của đường tròn đáy và A là một điểm trên đường tròn đó).
Ta suy ra: S xq = πrl = πl 2 cosα
Khối nón có chiều cao h = DO = lsin α . Do đó thể tích V của khối nón được tính theo công thức
Vậy :
Cho một hình nón có góc ở đỉnh bằng 60 ° , bán kính đáy bằng 2a, diện tích toàn phần của hình nón là
A. S t p = 20 πa 2
B. S t p = 12 πa 2
C. S t p = 8 πa 2
D. S t p = 10 πa 2
Cho hình nón có độ dài đường sinh bằng 4, góc giữa đường sinh và mặt đáy bằng 30 0 . Tính diện tích toàn phần S t p của hình nón.
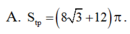
