Cho hàm số f(x)=-1/3x3 + 4x2-7x+2. Tập nghiệm của bất phương trình: f ' ( x ) ≥ 0 là
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) = 1 - 3 x + x 2 x - 1 . Tập nghiệm của bất phương trình f'(x) > 0 là:
A. R\{1}
B. ∅
C. 1 ; + ∞
D. R
Cho hàm số y = f ( x ) = ln ( 1 + x 2 + x ) .
Tập nghiệm của bất phương trình
f ( a - 1 ) + f ( ln a ) ≤ 0 là:
![]()
![]()
![]()
![]()
Cho hàm số f ( x ) = x 3 - 3 x + 2018 . Tập nghiệm của bất phương trình f'(x) > 0 là:
A. (-1;1)
B. [-1;1]
C. - ∞ ; - 1 ∪ 1 ; + ∞
D. ( - ∞ ; - 1 ] ∪ [ 1 ; + ∞ )
Đáp án C.
- Phương pháp:
+) Tính f'(x).
+) Sử dụng quy tắc trong trái ngoài cùng giải bất phương trình bậc hai.
- Cách giải:
+ Ta có:
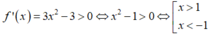
→ Vậy tập nghiệm của bất phương trình là 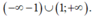
Cho hàm số f ( x ) = l n ( x 2 - 2 x + 3 ) . Tập nghiệm của bất phương trình f'(x)>0 là
A. ( 2 ; + ∞ ) .
B. ( - 1 ; + ∞ ) .
C. ( - 2 ; + ∞ ) .
D. ( 1 ; + ∞ ) .
Cho hàm số f ( x ) = 1 3 x 3 - x 2 + 2 x - 2009 . Tập nghiệm của bất phương trình f'(x) ≤ 0 là:
A. ∅
B. [-2;2]
C. 0 ; + ∞
D. R
Chọn A
- Ta có:
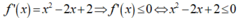
- Suy ra bất phương trình vô nghiệm.
Cho hàm số 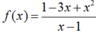 . Tập nghiệm của bất phương trình f’(x) > 0 là
. Tập nghiệm của bất phương trình f’(x) > 0 là
A. R \ {1}.
B. ∅.
C. (1; +∞).
D. R.
Cho hàm số f(x) = x2e-x. Bất phương trình f ' ( x ) ≥ 0 có tập nghiệm là:
![]()
![]()
![]()
![]()
Cho hàm số y = f x = 2 x 2 − 7 x + 6 x − 2 k h i x < 2 a + 1 − x 2 + x k h i x ≥ 2 . Biết a là giá trị để hàm số f(x) liên tục tại x 0 = 2 , tìm nghiệm nguyên của bất phương trình − x 2 + a x + 7 4 > 0 .
A. 1
B. 4
C. 3
D. 2
Đáp án D
Ta có lim x → 2 − f x = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − 2 x 2 − 7 x + 6 x − 2 = lim x → 2 − − 2 x − 3 = − 1
Và lim x → 2 − f x = lim x → 2 − a + 1 − x 2 + x = a − 1 4 ; f 2 = a − 1 4 .
Theo bài ra, ta có lim x → 2 + f x = lim x → 2 − f x = f 2 ⇒ a = − 3 4
Do đó, bất phương trình − x 2 + a x + 7 4 > 0 ⇔ − x 2 − 3 4 x + 7 4 > 0 ⇔ − 7 4 < x < 1.
Cho hàm số \(f(x) = \frac{1}{3}{x^3} - {x^2} - 3x + 1\). Tập nghiệm của bất phương trình \(f'(x) \le 0\) là
A. [1 ; 3].
B. \([ - 1;3]\).
C. \([ - 3;1]\).
D. \([ - 3; - 1]\)
Ta có: \(f'\left(x\right)=x^2-2x-3\)
\(f'\left(x\right)\le0\\ \Rightarrow x^2-2x-3\le0\\ \Leftrightarrow\left(x+1\right)\left(x-3\right)\le0\\ \Leftrightarrow-1\le x\le3\)