Tìm tất cả các nghiệm của phương trình log x + log ( x - 9 ) = 1
A. {10}
B. {9}
C. {1;9}
D. {-1;10}
Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt.
A. 6.
B. 2.
C. 3.
D. 5.
Cho phương trình log2(10x) - 2mlog10xx - log(10x2)=0 . Gọi S là tập chứa tất cả các giá trị nguyên của m thuộc [-10;10] để phương trình đã cho có đúng 3 nghiệm phân biệt . Số phần tử của tập S là
Tất cả các giá trị của tham số m để phương trình log m x = 2 log x + 1 có nghiệm là
Tổng tất cả các nghiệm của phương trình log 2 2 x - 2 log 2 x - 3 = 0 bằng
A. 2.
B. -3.
C. 17/2
D. 9/8
Tổng tất cả các nghiệm của phương trình log 2 2 x − 2 log 2 x − 3 = 0 bằng
A. 2 .
B. − 3 .
C. 17 2 .
D. 9 8 .
Tổng tất cả các nghiệm của phương trình log 3 2 x - 4 log 2 x . log 3 2 + 3 = 0 bằng
A. 4
B. 30
C. 81
D. 9
Cho phương trình 2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x Tổng tất cả các nghiệm thuộc đoạn 0 ; 20 π của phương trình bằng
A. 1150 3 π
B. 570 3 π
C. 880 3 π
D. 875 3 π
Cho phương trình 2 sin x - 1 3 tan x + 2 sin x = 3 - 4 cos 2 x . Tổng tất cả các nghiệm thuộc đoạn 0 ; 20 π của phương trình bằng
A. 1150 3 π
B. 570 3 π
C. 880 3 π
D. 875 3 π
Chọn D.
Phương pháp:
- Sử dụng các công thức nhân ba, phân tích tích thành tổng để biến đổi đơn giản phương trình.
- Giải phương trình, tìm nghiệm thỏa mãn bài toán và tính tổng các nghiệm.
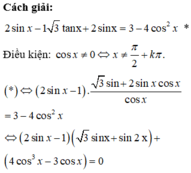
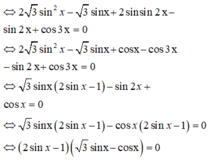
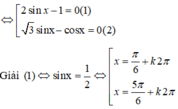
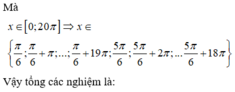
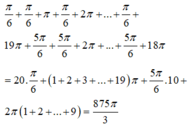
Cho phương trình 2 3 sin x + cos x = sin 2 x + 3 . Tổng tất cả các nghiệm của phương trình trong khoảng - 2 π , 2 π là:
A. - 2 π
B. - π
C. π
D.0
