Cho f, g là hai hàm liên tục trên đoạn [1;3] thoả: ∫ 1 3 f x + 3 g x d x = 10 , ∫ 1 3 2 f x - g x d x = 6 . Tính ∫ 3 f x + g x d x .
A. 7.
B. 6.
C. 8.
D. 9
Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [0;2].. Biết rằng F ( 0 ) = 0 , F ( 2 ) = 1 , G ( 0 ) = - 2 , G ( 2 ) = 1 và ∫ 0 2 F x g x d x = 3 . Tích phân ∫ 0 2 f x G x d x có giá trị bằng
A. 3
B. 0
C. -2
D. - 4
Chọn C.
Áp dụng công thức tích phân từng phần, ta có
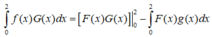
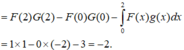
Cho hai hàm số liên tục f và g có nguyên hàm lần lượt là F và G trên đoạn [1;2]. Biết rằng F ( 1 ) = 1 , F ( 2 ) = 4 , G 1 = 3 2 , G 2 = 2 v à ∫ 1 2 f x G x d x = 67 12 . Tích phân ∫ 1 2 F x g x d x có giá trị bằng
A. 11 12
B. - 145 12
C. - 11 12
D. 145 12
Chọn A.
Áp dụng công thức tích phân từng phần, ta có
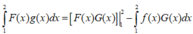

Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm của f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), (tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm).
- Vì F(x) và G(x) đều là nguyên hàm của f(x) nên tồn tại một hằng số C sao cho: F(x) = G(x) + C
- Khi đó F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).
Cho hàm số y = f ( x ) , y = g ( x ) liên tục trên đoạn [ a ; b ] ( a < b ) . Hình phẳng D giới hạn bởi đồ thị hai hàm số y = f ( x ) , y = g ( x ) và hai đường thẳng x = a, x= b có diện tích là
A. S D = ∫ a b f ( x ) − g ( x ) d x .
B. S D = ∫ a b f ( x ) − g ( x ) d x .
C. S D = π ∫ a b f ( x ) − g ( x ) d x .
D. S D = ∫ b a f ( x ) − g ( x ) d x .
Cho f(x) và g(x) là hai hàm số liên tục trên đoạn [1;3], thỏa mãn: ∫ 1 3 [ f ( x ) + 3 g ( x ) ] d x = 10 và ∫ 1 3 [ 2 f ( x ) - g ( x ) ] d x = 6 . Tính I = ∫ 1 3 [ f ( x ) + g ( x ) ] d x
A. I=8
B. I=9
C. I=6
D. I=7
Cho hai hàm số y=f(x) và y=g(x) là các hàm xác định và liên tục trên R và có đồ thị như hình vẽ bên (trong đó đường cong đậm hơn là của đồ thị hàm số y=f(x). Có bao nhiêu số nguyên m để phương trình f(1-g(2x-1))=m có nghiệm thuộc đoạn - 1 ; 5 2
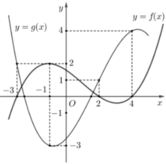
A. 8
B. 3
C. 6
D. 4
Cho hai hàm số y=f(x) và y=g(x) là hai hàm số liên tục trên ℝ có đồ thị hàm số y=f’(x) là đường cong nét đậm, đồ thị hàm số y=g’(x) là đường cong nét mảnh như hình vẽ. Gọi ba giao điểm A, B, C của y=f’(x) và y=g’(x) trên hình vẽ lần lượt có hoành độ là a, b, c. Tìm giá trị nhỏ nhất của hàm số h(x)=f(x)-g(x) trên đoạn [a;c]

A. m i n h x a ; c = h 0
B. m i n h x a ; c = h a
C. m i n h x a ; c = h b
D. m i n h x a ; c = h c
Cho hai hàm số liên tục f(x) và g(x) có nguyên hàm lần lượt là F(x) và G(x) trên [0; 2]. Biết F(0) = 0, F(2) = 1, G(2) = 1 và ∫ 0 2 F ( x ) g ( x ) d x = 3 . Tính tích phân hàm: ∫ 0 2 G ( x ) f ( x ) d x
A. I = 3.
B. I = 0.
C. I = -2.
D. I = -4.
Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.
Cho hàm số y=f(x) có đạo hàm, liên tục trên đoạn [-3;3] và đồ thị hàm số y=f' (x) như hình vẽ bên. Biết f(1)=6 và g(x)=f(x)- ( x + 1 ) 2 2 .
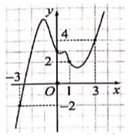
Kết luận nào sau đây là đúng
A. Phương trình g(x)=0 có đúng hai nghiệm thuộc [-3;3].
B. Phương trình g(x)=0 có đúng một nghiệm thuộc [-3;3].
C. Phương trình g(x)=0 không có nghiệm thuộc [-3;3].
D. Phương trình g(x)=0 có đúng ba nghiệm thuộc [-3;3].