Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của tứ diện đều ABCD cạnh bằng 1.
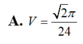
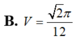
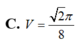
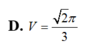
Tính thể tích V của khối cầu tiếp xúc với tất cả các cạnh của tứ diện đều ABCD cạnh bằng 1.
A. V = 2 π 24
B. V = 2 π 12
C. V = 2 π 8
D. V = 2 π 3
Đáp án A
Phương pháp: Xác định tâm mặt cầu ngoại tiếp khối chóp tam giác đều.
B1: Xác định hai trục của hai mặt phẳng bất kì (đường thẳng đi qua tâm đường tròn ngoại tiếp đáy và vuông góc với đáy).
B2: Xác định giao điểm I của hai trục đó. Khi đó I là tâm mặt cầu cần tìm.
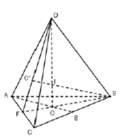
Cách giải: Gọi O và O’ lần lượt là tâm tam giác đều ABC và ACD thì D O ⊥ A B C ; B O ' ⊥ A C D
Gọi I = D O ∩ B O ' , ta dễ dạng chứng minh được I là tâm mặt cầu tiếp xúc với các cạnh của tứ diện đều.
Và R = IF là bán kính mặt cầu đó.
Kẻ BB’ qua I và song song với BD.
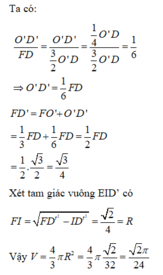
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
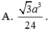
![]()
![]()
![]()
Cho tứ diện đều ABCD có cạnh bằng a. Thể tích của khối cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD bằng
A. 3 a 3 24 .
B. 2 π a 3 24 .
C. 2 2 a 3 9 .
D. 3 π a 3 8 .
Đáp án B
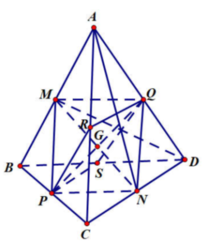
Gọi G là trọng tâm tứ diện ABCD. Ta chứng minh G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện.
Gọi M, N, P, Q, R, S lần lượt là trung điểm các cạnh AB, CD, BC, AD, AC, BD.
Ta có G là trung điểm của các đoạn MN, PQ, RS.
Δ A C D = Δ B C D ⇒ A N = B N ⇒ Δ N A B cân tại N ⇒ M N ⊥ A B
Tương tụ ta có M N ⊥ C D .
Ta có: P Q = R S = M N = A N 2 − A M 2 = a 3 2 2 − a 2 4 = a 2 2 .
Suy ra d G , A B = d G , C D = 1 2 M N = a 2 4 .
Chứng minh tương tự ta có d G , A C = d G , A D = d G , B D = d G , B C = a 2 4
Vậy G là tâm mặt cầu tiếp xúc với tất cả các cạnh của tứ diện ABCD.
Bán kính mặt cầu R = a 2 4 . Suy ra thể tích khối cầu là V = 4 3 π R 3 = 4 3 π a 2 4 3 = 2 π a 3 24 .
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
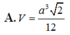
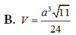
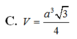
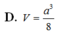
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Tính thể tích V của khối tứ diện ABCD
A. V = a 3 2 12
B. V = a 3 11 24
C. V = a 3 3 4
D. V = a 3 8
Cho tứ diện đều ABCD có cạnh 2a. Tính bán kính r của mặt cầu tiếp xúc với tất cả các mặt của tứ diện
A. r = a 6 12
B. r = a 6 8
C. r = a 6 6
D. r = a 6 3
Cho tứ diện đều ABCD có cạnh 2a. Tính bán kính r của mặt cầu tiếp xúc với tất cả các mặt của tứ diện.
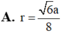
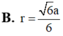
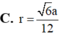
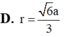
Cho tứ diện đều A B C D có cạnh 2a. Tính bán kính r của mặt cầu tiếp xúc với tất cả các mặt của tứ diện
A. r = 6 a 8
B. r = 6 a 6
C. r = 6 a 12
D. r = 6 a 3
Đáp án B
Bán kính mặt cầu nội tiếp tứ diện là r = 3 V S t p = 3. 2 a 3 2 12 4. 2 a 2 3 4 = a 6 6 .
Cho tứ diện đều ABCD có cạnh 2a. Tính bán kính r của mặt cầu tiếp xúc với tất cả các mặt của tứ diện
A. r = 6 a 8
B. r = 6 a 6
C. r = 6 a 12
D. r = 6 a 3
Đáp án B
Gọi H và K lần lượt là hình chiếu của A xuống (BCD) và (ABC).
A H ∩ D K = O . Khi đó O là tâm mặt cầu nội tiếp tứ diện
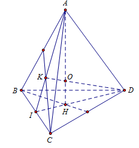
Ta có: D H = 2 3 2 a 2 − a 2 = 2 a 3 ; I K = 1 2 . 2 a 3 = a 3
D K = D I 2 − I K 2 = 4 a 2 − a 2 − a 3 2 = 2 a 6 3
Ta có: Δ D O H ~ Δ D I K ⇒ O H D H = I K D K
⇒ O H = D H . I K D K ⇒ r = O H = 2 a 3 . a 3 2 a 6 3 = a 6 6
Cách 2: Ta có: cos A I H ^ = H I A I = 1 3
⇒ O H = H I tan A I H ^ 2 = 2 a 3 6 . 1 2 = a 6 6 = r