Cho số phức z thỏa mãn điều kiện z + 1 i - z ¯ là số thực. Khi đó môđun của z có giá trị nhỏ nhất bằng
![]()
![]()
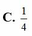
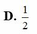
Cho số phức z thỏa mãn điều kiện z - 3 + 2 i = z - i Giả sử w là số phức có môđun nhỏ nhất trong các số phức z thỏa mãn điều kiện trên. Tính môđun của w
![]()
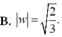
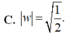
![]()
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + + z ) z ¯ .
A. -2
B. 0.
C. -1
D. 1
Cho số phức z thỏa mãn điều kiện ( 3 + 2 i ) z + ( 2 - i ) 2 = 4 + i . Tìm phần ảo của số phức w = ( 1 + z ) z ¯ .
![]()
![]()
![]()
![]()
Cho số phức z thỏa mãn điều kiện (1+i) z ¯ - 1 - 3i = 0. Tìm phần ảo của số phức w = 1 - zi + z ¯
A. -i
B. -1
C. 2
D. -2i
Đáp án C
giả sử ![]()
The giả thiết, ta có
![]()
![]()
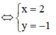
Suy ra ![]()
Ta có ![]()
![]()
Vậy chọn phần ảo là – 1
Cho số phức z thỏa mãn điều kiện: z - 1 + 2 i = 5 và w = z + 1 + i có môđun lớn nhất. Số phức z có môđun bằng:
A. 2 5
B. 3 2
C. 6
D. 5 2
Cho số phức z thỏa mãn điều kiện: z - 1 + 2 i = 5 và w = z +1 +i có môđun lớn nhất. Số phức z có môđun bằng:
A. 6
B. 3 2
C. 5 2
D. 2 5
Cho số phức z thỏa mãn điều kiện | z - 1 + 2 i | = 5 và w=z+1+i có môđun lớn nhất. Số phức z có môđun bằng
A. 2 5
B. 3 2
C. 6
D. 5 2
Cho số phức z thỏa mãn điều kiện z - 1 = 2 . Tìm giá trị lớn nhất của T = z + i + z - 2 - i
A. m a x T = 8 2
B. m a x T = 4
C. m a x T = 4 2
D. m a x T = 8 2
Có bao nhiêu số phức z thỏa mãn điều kiện z + i + 1 = z - 2 i v ầ z = 1
A. 0
B. 2
C. 1
D. 4
Cho số phức z thỏa mãn điều kiện (1 - i)(2 + i)z + 1 - i = (5 - i)(1 + i). Tính môđun của số phức w = 1 + 2 z + z 2
A. 8
B. 64
C. 2 2
D. 5
Đáp án A
Ta có z = 5 - i 1 + i + i - 1 1 - i 2 + i = 1 + 2 i ⇒ w = 8 i ⇒ w = 8 .