Số mặt phẳng đối xứng của tứ diện đều là
A.10
B. 8
C.6
C.6
Hỏi hình tạo bởi 6 đỉnh là 6 trung điểm của các cạnh một tứ diện đều có bao nhiêu mặt phẳng đối xứng?
A. 6
B. 3
C. 4
D. 9
Phương pháp:
Sử dụng lý thuyết khối đa diện để làm bài toán.
Cách giải:
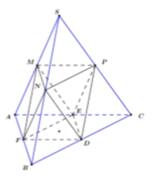
Khối đa diện được tạo từ 6 đỉnh là 6 trung điểm của các cạnh của tứ diện đều là khối bát diện đều có 6 đỉnh, 12 cạnh và 8 mặt.
Khối bát diện đều là khối đa diện có 9 mặt đối xứng.
Chọn: D
Số mặt phẳng đối xứng của tứ diện đều là:
A. 4.
B. 8.
C. 6.
D. 10.
Chọn C.
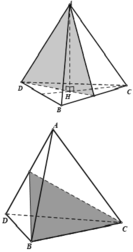

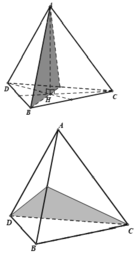
Tứ diện đều có mặt phẳng đối xứng là mặt phẳng tạo bởi một cạnh với trung điểm của cạnh đối diện của nó.
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 7
A. 7
C. 9
D. 6
Số mặt phẳng đối xứng của hình tứ diện đều là?
A. 4 mặt phẳng
B. 6 mặt phẳng
C. 8 mặt phẳng
D. 10 mặt phẳng
Đáp án B.
Hướng dẫn giải:
Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện

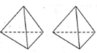
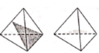
Vậy hình tứ diện đều có 6 mặt phẳng đối xứng
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 6
B. 7
C. 9
D. 9
Đáp án A
Tứ diện đều có 6 mặt phẳng đối xứng đó là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối diện
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 6
B. 7
C. 9
D. 10
Đáp án A
Tứ diện đều có 6 mặt phẳng đối xứng đó là các mặt phẳng đi qua một cạnh và trung điểm của cạnh đối diện
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 7
B. 8
C. 9
D. 6
Số mặt phẳng đối xứng của hình tứ diện đều là:
A. 6
B. 2
C. 3
D. 9
Số mặt phẳng đối xứng của khối tứ diện đều là
A. 7
B. 8
C. 9
D. 6