Nếu tam giác ABC vuông tại C và có sinA = 2/3 thì tgB bằng:
( A ) 3 5 ( B ) 5 3 ( C ) 2 5 ( D ) 5 2
Nếu tam giác ABC vuông tại C và có sinA = 2/3 thì tgB bằng:
( A ) 3 5 ( B ) 5 3 ( C ) 2 5 ( D ) 5 2
\(\frac{3}{4}=tanB=\frac{AC}{AB}\Rightarrow AC=\frac{3}{4}AB\)
\(BC^2=AB^2+AC^2\)(định lí Pythagore)
\(=AB^2+\frac{9}{16}AB^2=\frac{25}{16}AB^2\)
\(\Rightarrow AB^2=10^2.\frac{16}{25}\Rightarrow AB=8\left(cm\right)\)
\(\Rightarrow AC=\frac{3}{4}AB=6\left(cm\right)\)
Tam giác ABC vuông tại A có BC=20cm, AB=10cm
1. Giải tam giác ABC vuông và tính độ dài đường cao AH
2. Cminh: tgB, Sin B=\(\dfrac{HC}{AB}\)
3. Kẻ phân giác của góc BAC cắt BC tại I. Tính HI
\(AC=\sqrt{BC^2-AB^2}=10\sqrt{3}\left(cm\right)\left(pytago\right)\\ \sin B=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}=\sin60^0\Rightarrow\widehat{B}=60^0\\ \widehat{C}=90^0-\widehat{B}=30^0\\ 2,\sin B\cdot\tan B=\dfrac{AC}{AB}\cdot\dfrac{AC}{BC}=\dfrac{AC^2}{AB\cdot BC}=\dfrac{HC\cdot BC}{AB\cdot BC}=\dfrac{HC}{AB}\\ 3,\dfrac{CI}{IB}=\dfrac{AC}{AB}=\sqrt{3}\Leftrightarrow CI=\sqrt{3}IB\\ CI+IB=BC=20\\ \Rightarrow\left(\sqrt{3}+1\right)IB=20\Leftrightarrow IB=\dfrac{20}{\sqrt{3}+1}=10\sqrt{3}-10\left(cm\right)\\ HB=\dfrac{AB^2}{BC}=5\left(cm\right)\left(HTL\right)\\ IH=IB-HB=10\sqrt{3}-15\left(cm\right)\)
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA
\(\sin^2\widehat{A}+\cos^2\widehat{A}=1\Leftrightarrow\cos^2\widehat{A}=1-\left(\dfrac{3}{5}\right)^2=1-\dfrac{9}{25}=\dfrac{16}{25}\\ \Leftrightarrow\cos\widehat{A}=\dfrac{4}{5}\\ \tan\widehat{A}=\dfrac{\sin\widehat{A}}{\cos\widehat{A}}=\dfrac{3}{4}\\ \Rightarrow\cot\widehat{A}=\dfrac{1}{\tan\widehat{A}}=\dfrac{4}{3}\)
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA.
Cho tam giác ABC vuông tại C có sinA=3/5 .không tính số đo góc A.Hãy tính cosA,tanA,cotA.
Bài 1: Cho tam giác ABC vuông tại A, biết \(tgB=\frac{4}{3}\)và BC = 10. Tính AB, AC.
Bài 2: Cho tam giác ABC cân tại A, AB=AC=17, BC=16. Tính đường cao AH và góc A, góc B của tam giác ABC.
Bài 3: Cho tam giác ABC có \(\widehat{B}=60\) ,các hình chiếu vuông góc của AB và AC lên BC theo thứ tự bằng 12 và 18. Tính các góc và đường cao của tam giác ABC.
Bài 1: Cho tam giác ABC cân tại A có các đường trung tuyến BE và CD . Chứng minh rằng BE bằng CD
Bài 2: Cho tam giác ABC có đường trung tuyến BE và CD, biết BE = CD . Chứng minh rằng tam giác ABC cân tại A
Bài 3: Cho tam giác ABC chứng minh rằng a) Nếu tam giác ABC vuông góc tại A , có trung tuyến AM =1/2 BC
b) Nếu trung tuyến AM =1/2 BC thì tam giác ABC vuông góc tại A
Nếu tam giác ABC vuông tại C và có \(\sin A=\dfrac{2}{3}\) thì tgB bằng :
(A) \(\dfrac{3}{5}\) (B) \(\dfrac{\sqrt{5}}{3}\) (C) \(\dfrac{2}{\sqrt{5}}\) (D) \(\dfrac{\sqrt{5}}{2}\)
Hãy chọn câu trả lời đúng ?
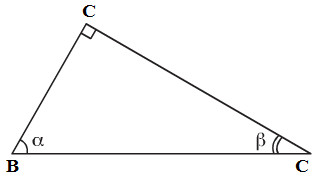
Trong tam giác vuông ABC (\(\widehat{C}=90^o\)), ta có:
sinA=BC/AB=2/3⇒AB=3/2 BC
Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có:
\(AC=\sqrt{AB^2-BC^2}=\sqrt{\left(\dfrac{3}{2}BC\right)^2-BC^2}=\dfrac{BC\sqrt{5}}{2}\)
Ta có:
\(\tan B=\dfrac{AC}{BC}=\dfrac{\dfrac{BC\sqrt{5}}{2}}{BC}=\dfrac{\sqrt{5}}{2}\)
Chọn đáp án D
Trong tam giác vuông ABC , ta có:
Áp dụng định lí Py-ta-go trong tam giác vuông ABC, ta có:
Ta có:
Chọn đáp án D