Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a với SA = a 2 , SB = a 3 2 , B A D ^ = 60 ∘ và mặt phẳng (SAB) vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là trung điểm của AB, BC. Thể tích tứ diện K.SDC có giá trị là:

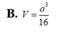
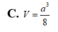
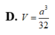
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, ABC = 60 ° cạnh bên SA = a 2 và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).
A. 90 °
B. 30 °
C. 45 °
D. 60 °
Chọn B.
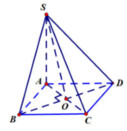
Gọi O = AC ∩ BD. Vì ABCD là hình thoi nên BO ⊥ AC(1). Lại do:
![]()
Từ (1) và (2) ta có:BO ⊥ (SAC)
![]()
Ta có: ![]()
Vì ABCD là hình thoi có ABC = 60 ° nên tam giác ABC đều cạnh a
![]()
Trong tam giác vuông SBO ta có:
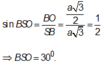
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa mặt bên hình chóp S.ABCD và mặt phẳng đáy có tang bằng:
A. 1
B. 3
C. 3 2
D. Đáp án khác
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng:
A. (SAD)
B. (SBD)
C. (SDC)
D. (SBC)
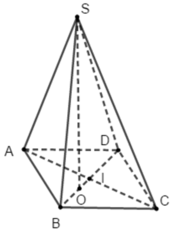
Gọi I là giao điểm của AC và BD.
Từ S vẽ SO ⊥ (ABCD)
⇒ OA = OB = OC (là hình chiếu của các đường xiên bằng nhau)
⇒ O là tâm đường tròn ngoại tiếp tam giác ABC
Ta có: BI là đường trung tuyến của tam giác ABC nên O nằm trên đường thẳng BI hay
Vậy: SO ⊂ (SBD) và SO ⊥(ABCD) ⇒ (SBD) ⊥(ABCD)
Đáp án B
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Góc giữa hai mặt bên hình chóp S.ABCD và mặt phẳng đáy có tan bằng:
A. 1
B. 3
C. 3 2
D. 2 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 0 , cạnh bên S A = a 2 và SA vuông góc với ABCD. Tính góc giữa SB và (SAC).
A. 90 0
B. 30 0
C. 45 0
D. 60 0
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và SA = SB = SC = a.
Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD) vì:
A. AC ⊂ (SAC) và AC ⊥ (SBD) do AC ⊥ SO và AC ⊥ BD
B. AC ⊂ (ABCD) và AC ⊥ (SBD) do AC ⊥ SO và AC ⊥ BD
C. AC ⊂ (SAC) và AC ⊥ SO ⊂ (SBD)
D. AC ⊂ (ABCD) và AC ⊥ SO ⊂ (SBD) và góc AOS bằng 90 o
Cho khối chóp S . A B C D có đáy A B C D là hình thoi cạnh a, S A = S B = S C = a , cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S . A B C D bằng
A. a 3 8
B. a 3 2
C. 3 a 3 8
D. a 3 4
Đáp án là D.
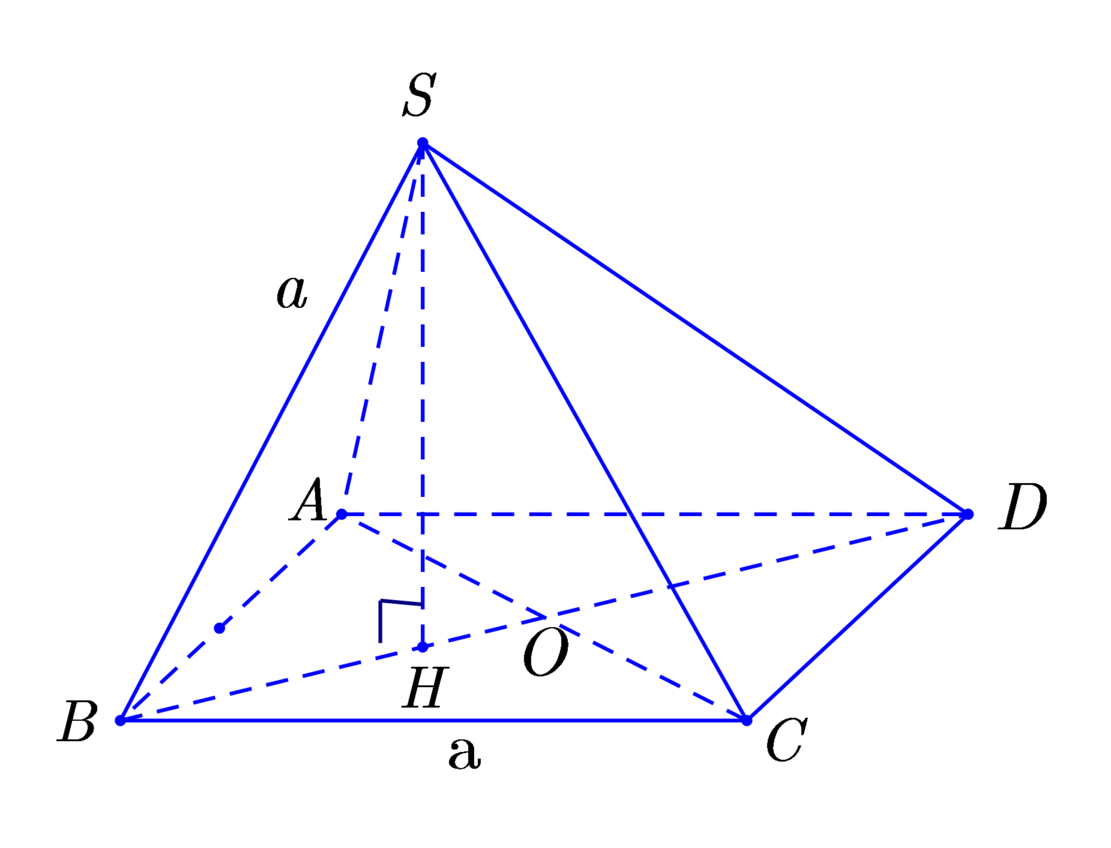
Khi SD thay đổi thi AC thay đổi. Đặt AC = x.
Gọi O = A C ∩ B D .
Vì S A = S B = S C nên chân đường cao SH trùng với tâm đường tròn ngoại tiếp tam giác ABC.
⇒ H ∈ B O
Ta có: O B = a 2 − x 2 2 = 4 a 2 − x 2 4 = 4 a 2 − x 2 2
S A B C = 1 2 O B . A C = 1 2 x . 4 a 2 − x 2 2 = x 4 a 2 − x 2 4
H B = R = a . a . x 4 S A B C = a 2 x 4. x 4 a 2 − x 2 4 = a 2 4 a 2 − x 2
S H = S B 2 − B H 2 = a 2 − a 4 4 a 2 − x 2 = a 3 a 2 − x 2 4 a 2 − x 2
S H = S B 2 − B H 2 = a 2 − a 4 4 a 2 − x 2 = a 3 a 2 − x 2 4 a 2 − x 2
= 1 3 a x . 3 a 2 − x 2 ≤ 1 3 a x 2 + 3 a 2 − x 2 2 = a 3 2
Khối chóp S.ABCD có đáy ABCD là hình thoi cạnh a. SA=SB=SC=a, Cạnh SD thay đổi. Thể tích lớn nhất của khối chóp S.ABCD là:
A. a 3 8
B. a 3 4
C. 3 a 3 8
D. a 3 2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, S A ⊥ ( A B C D ) và SB=a 3 . Tính thể tích khối chóp S.ABCD
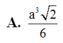
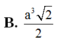
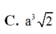
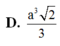
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, góc A B C ^ = 60 ° . Biết SA = SB = SC = a. Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng:
A. 60 °
B. 30 °
C. 45 °
D. 90 °
Chọn D.
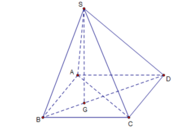
- Gọi G là trọng tâm tam giác ABC.
- Hình chóp S.ABC là hình chóp đều nên SG ⊥ (ABC).
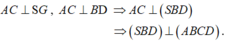
→ Góc giữa hai mặt phẳng (SBD) và (ABCD) bằng 90 °