Cho hình thang cân ABCD có các cạnh AB=2a; CD=4a và cạnh bên AD=BC=3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó.
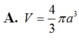


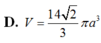
Cho hình thang cân ABCD có các cạnh AB=2a, CD=4a và cạnh bên AD=BC=3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD xung quanh trục đối xứng của nó.
A. V = 4 3 π a 3
B. V = 4 + 10 2 3 π a 3
C. V = 10 2 3 π a 3
D. V = 14 2 3 π a 3
Cho hình thang cân ABCD có các cạnh đáy AB = 2a, CD = 4a và cạnh bên AD = BC = 3a. Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
A. V = 4 3 πa 3
B. V = 4 + 10 2 3 πa 3
C. V = 10 2 3 πa 3
D. V = 14 2 3 πa 3
Đáp án D
Khi quay hình thang cân ABCD quanh trục đối xứng ta được hình nón cụt có chiều cao h = 2 a 2 và bán kính 2 đáy là R 1 = a , R 2 = 2 a .
Vậy thể tích cần tính là V = πh 3 R 1 2 + R 2 2 + R 1 R 2 = 14 2 3 πa 3
Cho hình thang cân ABCD có các cạnh đáy ![]() và cạnh bên AD=BC=2a Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
và cạnh bên AD=BC=2a Tính theo a thể tích V của khối tròn xoay thu được khi quay hình thang cân ABCD quanh trục đối xứng của nó.
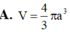
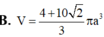
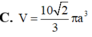
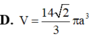
BÀI 3; Cho hình thang cân ABCD ( AB // CD ), có góc A = 2 góc C. Tính các góc của hình thang ABCD.
BÀI 4; Cho hình thang cân ABCD có AB // CD. Các đường thẳng chứa hai cạnh bên cắt nhau tại O. CM : OA = OB
Do AB // CD ( GT )
⇒^A+^C=180o
⇒2^C+^C=180o
⇒3^C=180o
⇒^C=60o
⇒ ^A = 60o * 2 = 120o
Do ABCD là hình thang cân
⇒ ^C = ^D
Mà ^C = 60o
⇒ ^D = 60o
AB // CD ⇒ ^D + ^B = 180o
⇒ˆB=180o − 60o = 120o
Vậy ^A = ^B = 120o ; ^C= ^D = 60o
Xét 2 tam giác : Tam giác ADB và tam giác BCA có :
AB : Cạnh chung
^DAB=^CBA (Tính chất của hình thang cân)
AC = BD ( Tính chất của hình thang cân)
⇒ ΔADB = ΔBCA ( c−g−c)
⇒ ^CAB = ^DBA (2 góc tương ứng)
⇒ ^OAB = ^OBA
=> Tam giác OAB cân
=> OA = OB
=> Điều phải chứng minh
Cho một hình thang cân ABCD có cạnh đáy A B = 2 a , C D = 4 a , cạnh bên A D = B C = 3 a . Hãy tính thể tích của khối tròn xoay sinh bởi hình thang đó khi quay quanh trục đối xứng của nó.
A. 4 2 π a 3 3
B. 56 2 π a 3 3
C. 16 2 π a 3 3
D. 14 2 π a 3 3
1, Cho hình thang cân ABCD có đáy nhỏ AB, đường cao AH=2cm. Biết HC=3,5cm và HD=1,5cm. Tính chu vi của hình thang này 2, Cho hình thang cân ABCD có cạnh bên AD=5cm, các cạnh đáy AB=6cm và CD=14cm. Tính chiều cao của hình thang. XIN HÃY GIÚP MÌNH Ạ, xin cảm ơn 🌹❤️
Bài 1: Cho hình thang cân ABCD ( AB// CD ) có góc A= 2 góc C. Tính số đo các góc hình thang
Bài 2: Cho hình thang cân ABCD ( AB// CD ) có góc A= 3 góc D. Tính số đo các góc của hình thang
Bài 3: Cho hình tam giác ABC cân tại A. Qua điểm M trên cạnh AB kẻ đường thằng song song với BC cắt cạnh ACtại N
1, Tứ giác BMNC là hình gì? Vì sao?
2, So sánh diện tích MNB và diện tích MNC
3, CM diện tích ABN= diện tích ACM
Bafi1: Do AB // CD ( GT )
⇒ˆA+ˆC=180o
⇒2ˆC+ˆC=180o
⇒3ˆC=180o
⇒ˆC=60o
⇒ˆA=60o.2=120o
Do ABCD là hình thang cân
⇒ˆC=ˆD
Mà ˆC=60o
⇒ˆD=60o
AB // CD ⇒ˆD+ˆB=180o
⇒ˆB=180o−60o=120o
Vậy ˆA=ˆB=120o;ˆC=ˆD=60o
Bài 2:
Ta có; AB//CD
\(\Rightarrow\)góc BAD+ góc ADC= \(180^o\)
^A=3. ^D \(\Rightarrow\)\(\dfrac{A}{3}\)=^D
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\dfrac{A}{3}=\dfrac{D}{1}=\dfrac{A+D}{3+1}=\dfrac{180^O}{4}=45^O\)
\(\Rightarrow\)^A= \(135^O\)
\(\Rightarrow\)^D=\(45^o\)
\(\Rightarrow B=A=135^o\)
\(\Rightarrow C=D=45^o\)
cho hình thang cân ABCD có đọ dài đáy AB bằng 4cm, độ dài đáy CD gấp đôi độ dài đáy AB, độ dài cạnh bên AC bằng 5cm. Tính tổng độ dài các cạnh của hình thang cân ABCD
Độ dài đáy CD là:
\(4\times2=8cm\)
Tổng độ dài các cạnh của hình thang cân ABCD là:
\(4+8+5\times2=22cm\)
Cho hình thang cân ABCD có đáy AB= 125 cm, DC= 65cm , cạnh bên AB = 50cm
a, Tính diện tích hình thang cân ABCD
b, Tính các góc của ht ABCD
c, Tính các đường chéo
Chỉnh sửa xíu nhé: cạnh bên AD = 50cm
kẻ =DH và CK vuông góc với AB
ta có :
AB = BH + HK+ AK
vì là hình thang cân nên DC = HK ; BH =AK = \(\frac{1}{2}\)(AB-HK)
=> HK = 65 cm
AK = BH = \(\frac{1}{2}\)(AB - HK)= \(\frac{1}{2}\)(125-65)= 30
=> AK = 30 cm; BH = 30cm
Áp dụng định lí py-ta-go vào tam giác vuông DAK, ta có:
DA2= AK2+DK2
=> DK2 = DA2 -AK2
= 502 - 302
= 1600
=> DK = \(\sqrt{1600}\)=40 cm
a) Diện tích hình thang ABCD là:
SABCD= \(\frac{1}{2}\)DK(DC+AB) =\(\frac{1}{2}\)40(65+125)=3800cm2
câu b phải có 1 góc ms tìm đc các góc còn lại chứ bạn sửa lại rồi mk làm cho