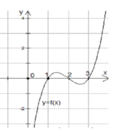
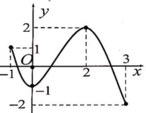
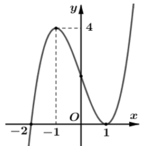
Hàm số y f(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng? A. Đồ thị hàm số có tiệm cận đứng là x 1 và tiệm cận ngang là y -2. B. Hàm số đồng biến trên các khoảng (-∞; -2), (-2; +∞). C. Đồ thị hàm số cắt trục hoành tại điểm M(0; -1). D. Hàm số nghịch biến trên các khoảng (-∞; -2), (-2; +∞).
Đọc tiếp
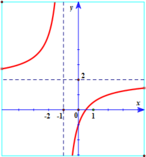
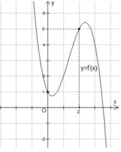
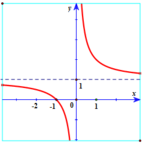
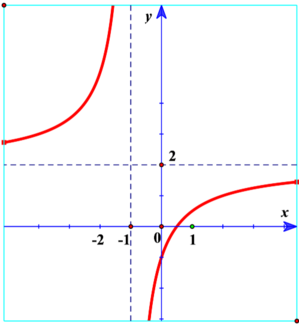
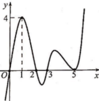
Hàm số y = f(x) có đồ thị như hình vẽ bên. Khẳng định nào sau đây là khẳng định đúng?
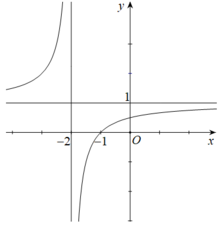
A. Đồ thị hàm số có tiệm cận đứng là x = 1 và tiệm cận ngang là y = -2.
B. Hàm số đồng biến trên các khoảng (-∞; -2), (-2; +∞).
C. Đồ thị hàm số cắt trục hoành tại điểm M(0; -1).
D. Hàm số nghịch biến trên các khoảng (-∞; -2), (-2; +∞).