Giả sử hàm số f ( x ) = a x 2 + b x + x e - x là một nguyên hàm của hàm số g ( x ) = x 1 - x e - x . Giá trị của biểu thức A = a + 2 b + 3 c bằng
A. 3
B. 4
C. 6
D. 9
Giả sử f(x) là hàm số liên tục trên đoạn [a; b], F(x) và G(x) là hai nguyên hàm của f(x). Chứng minh rằng F(b) – F(a) = G(b) – G(a), (tức là hiệu số F(b) – F(a) không phụ thuộc việc chọn nguyên hàm).
- Vì F(x) và G(x) đều là nguyên hàm của f(x) nên tồn tại một hằng số C sao cho: F(x) = G(x) + C
- Khi đó F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).
Giả sử F(x) là một nguyên hàm của hàm số 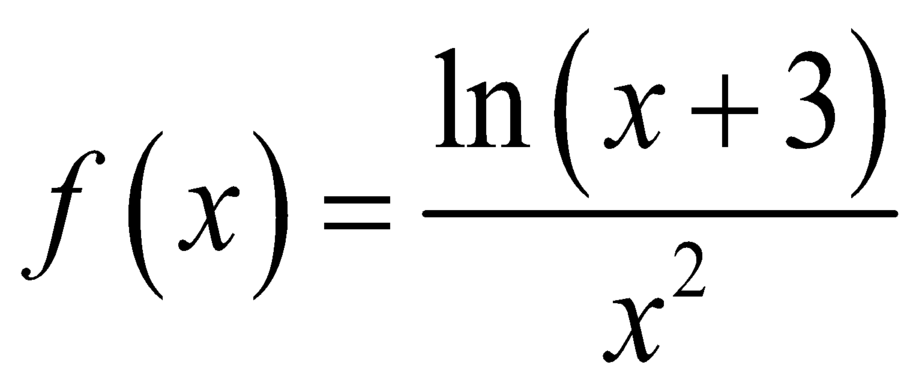 thỏa mãn F(-2) + F(1) = 0 và F(-1) + F(2) = 0, với a,b là các số hữu tỷ.
thỏa mãn F(-2) + F(1) = 0 và F(-1) + F(2) = 0, với a,b là các số hữu tỷ.
Giá trị của 3a+6b bằng
A. -4
B. 5
C. 0
D. -3
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
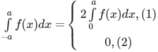
(1) : nếu f là hàm số chẵn
(2): nếu f là hàm số lẻ.
Áp dụng để tính:
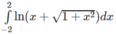
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
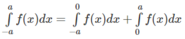
Đổi biến x = - t đối với tích phân
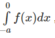
Ta được:
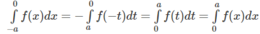
Vậy
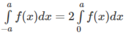
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì 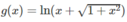
là hàm số lẻ trên đoạn [-2; 2] nên 
Cho hàm số y = f(x) liên tục trên [a;b]. Giả sử hàm số u = u(x) có đạo hàm liên tục trên [a;b] và u ( x ) ∈ [ α ; β ] ∀ x ∈ [ a ; b ] hơn nữa f(u) liên tục trên đoạn [a;b]. Mệnh đề nào sau đây là đúng?
A. ∫ a b f ( u ( x ) ) u ' d x = ∫ u ( a ) u ( b ) f ( u ) d u
B. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
C. ∫ u ( a ) u ( b ) f ( u ( x ) ) u ' d x = ∫ a b f ( u ) d u
D. ∫ a b f ( u ( x ) ) u ' d x = ∫ a b f ( x ) d x
Phương pháp: Sử dụng phương pháp đổi biến, đặt t = u(x)
Cách giải:
Đặt
![]()
Đổi cận 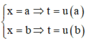
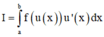

Biết F(x) là một nguyên hàm của hàm số f ( x ) = 10 x 3 - 7 x + 2 2 x - 1 thỏa mãn F(1) = 5. Giả sử rằng F ( 3 ) = a + b 5 , trong đó a,b là các số nguyên. Tính tổng bình phương của a và b
A. 121.
B. 73.
C. 265.
D. 361.
Biết F (x) là một nguyên hàm của hàm số f ( x ) = 10 x 3 - 7 x + 2 2 x - 1 thỏa mãn F(1) = 5. Giả sử rằng F(3) = a + b 5 , trong đó a , b là các số nguyên. Tính tổng bình phương của a và b.
A. 121
B. 73
C. 265
D. 361
Cho hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}.\)
a) Giả sử \({x_0} \in \mathbb{R}.\) Hàm số \(f\left( x \right)\) có liên tục tại điểm \({x_0}\) hay không?
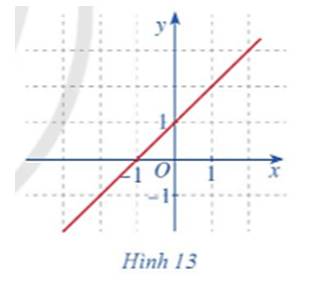
b) Quan sát đồ thị hàm số \(f\left( x \right) = x + 1\) với \(x \in \mathbb{R}\) (Hình 13), nếu nhận xét về đặc điểm của đồ thị hàm số đó.
a) Ta có \(f\left( {{x_0}} \right) = {x_0} + 1;\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = \mathop {\lim }\limits_{x \to {x_0}} \left( {x + 1} \right) = \mathop {\lim }\limits_{x \to {x_0}} x + 1 = {x_0} + 1\)
\( \Rightarrow \mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\)
Vậy hàm số \(f\left( x \right)\) liên tục tại \({x_0}.\)
b) Dựa vào đồ thị hàm số ta thấy: Đồ thị hàm số là một đường thẳng liền mạch với mọi giá trị \(x \in \mathbb{R}.\)
Giả sử hàm số f(x) liên tục trên đoạn [a; b]. Chứng minh rằng:
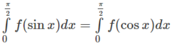
Đổi biến số: x = π/2 − t,
ta được: 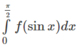
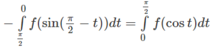
Hay
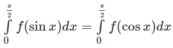
Biết F(x) là một nguyên hàm của hàm số f x = 6 x 2 + 13 x + 11 2 x 2 + 5 x + 2 thỏa mãn F(2)=7. Giả sử rằng F 1 2 = 5 2 + a ln 2 − b ln 5 , trong đó a, b là các số nguyên. Tính trung bình cộng của a và b.
A. 8
B. 3
C. 10
D. 5
Giả sử hàm số f(x) liên tục trên đoạn [-a; a]. Chứng minh rằng:
∫ - a a f x d x = 2 ∫ 0 a f x d x 1 0 2
(1) : nếu f là hàm số chẵn
(2): nếu f là hàm số lẻ.
Áp dụng để tính: ∫ - 2 2 ln x + 1 + x 2 d x
Giả sử hàm số f(x) là hàm số chẵn trên đoạn [-a; a], ta có:
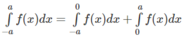
Đổi biến x = - t đối với tích phân
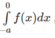
Ta được:
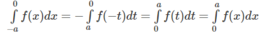
Vậy
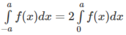
Trường hợp sau chứng minh tương tự. Áp dụng:
Vì ![]()
là hàm số lẻ trên đoạn [-2; 2] nên ![]()