Cho hình hộp ABCD.A'B'C'D' có thể tích bằng 12 c m 3 Tính thể tích của tứ diện AB'CD'
A. 2 c m 3 c m 3
B. 3 c m 3
C. 4 c m 3
D. 5 c m 3
PB
Những câu hỏi liên quan
Hình hộp chữ nhật ABCD.ABCD có thể tích V bằng bao nhiêu nếu biết thể tích tứ diện ABCD bằng
a
3
2
? A. 2
a
3
B.
3
a
3
2
C. 3
a
3
D.
a
3
Đọc tiếp
Hình hộp chữ nhật ABCD.A'B'C'D' có thể tích V bằng bao nhiêu nếu biết thể tích tứ diện AB'CD' bằng a 3 2 ?
A. 2 a 3
B. 3 a 3 2
C. 3 a 3
D. a 3
Cho hình hộp ABCD A'B'C'D' có thể tích bằng 12 c m 3 . Tính thể tích khối tứ diện AB'CD'.
A. 2 cm3
B. 3 cm3
C. 4 cm3
D. 5 cm3.
Đáp án C
Ta có V A B ' C D ' = V A B C D . A ' B ' C ' D ' − V A B B ' C − V B ' C ' C D ' − V A D C D ' − V A A ' B ' D '
= 12 − 1 6 .4. V A B C D . A ' B ' C ' D ' = 12 − 1 6 .4.12 = 4
Đúng 0
Bình luận (0)
Cho hình hộp chữ nhật ABCD.ABCD có ABa, AA2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
π
a
3
2
Tính thể tích V của hình hộp chữ nhật ABCD.ABCD.
Đọc tiếp
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB=a, AA'=2a Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 π a 3 2 Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
Cho hình hộp chữ nhật ABCD.ABCD có AB a, AA 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD là
9
πa
3
2
. Tính thể tích V của hình hộp chữ nhật ABCD.ABCD. A.
V
9
a
3
4
B.
V
4
a
3
C. ...
Đọc tiếp
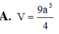
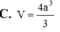
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, AA' = 2a. Biết thể tích hình cầu ngoại tiếp tứ diện ABCD' là 9 πa 3 2 . Tính thể tích V của hình hộp chữ nhật ABCD.A'B'C'D'.
A. V = 9 a 3 4
B. V = 4 a 3
C. V = 4 a 3 3
D. V = 2 a 3
Đáp án B
Thể tích khối cầu ngoại tiếp tứ diện ABCD’ chính là thể tích khối cầu ngoại tiếp hình hộp chữ nhật ABCD.A’B’C’D’. Khi đó, bán kính khối cầu ngoại tiếp là R = A C ' 2 .
Ta có V = 4 3 πR 3 = 4 3 π . AC ' 3 8 = 9 2 πa 3 ⇒ AC ' 3 = 27 a 3 ⇒ AC ' = 3 a .
Mặt khác A C ' 2 = A B 2 + A D 2 + A A ' 2 ⇒ A D 2 = ( 3 a 2 ) - a 2 - ( 2 a ) 2 = 4 a 2 ⇒ A D = 2 a .
Vậy thể tích của hình hộp chữ nhật ABCD.A'B'C'D' là V = A A ' . A B . A D = a . 2 a . 2 a = 4 a 3 .
Đúng 0
Bình luận (0)
Cho hình hộp ABCD.ABCD có thể tích là V. Tính thể tích của khối tứ diện theo V.
A
.
1
6
V
B
.
2
3
V
C
.
1
3
V
D
.
1
2
V
Đọc tiếp
Cho hình hộp ABCD.A'B'C'D' có thể tích là V. Tính thể tích của khối tứ diện theo V.
A . 1 6 V
B . 2 3 V
C . 1 3 V
D . 1 2 V
Cho hình lập phương
A
B
C
D
.
A
B
C
D
cạnh a. Xét tứ diện ABCD. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được. A.
a
2
3
.
B. ...
Đọc tiếp
Cho hình lập phương A B C D . A ' B ' C ' D ' cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được.
A. a 2 3 .
B. 2 a 2 3 .
C. a 2 2 .
D. 3 a 2 4 .
Cho hình lập phương ABCD.ABCD cạnh a. Xét tứ diện ABCD. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
Đọc tiếp
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
Cho hình lập phương ABCD.ABCD cạnh a. Xét tứ diện ABCD. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được A.
a
2
3
.
B.
2
a
2
3
.
C.
a...
Đọc tiếp
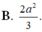
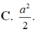
Cho hình lập phương ABCD.A'B'C'D' cạnh a. Xét tứ diện AB'CD'. Cắt tứ diện đó bằng mặt phẳng đi qua tâm của hình lập phương và song song với mặt phẳng (ABC). Tính diện tích của thiết diện thu được
A. a 2 3 .
B. 2 a 2 3 .
C. a 2 2 .
D. 3 a 2 4 .
Cho khối hộp ABCD.A'B'C'D có thể tích bằng 9. Tính thể tích khối tứ diện ACB'D'.
A. 3
B. 9 2
C. 6
D. 27 4
