Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình x - 1 2 = y - 5 = z - 3 4 . Viết phương trình mặt phẳng α chứa trục Oy và song song với đường thẳng d
A. -2x + y = 0
B. x - 2z = 0
C. 2x - z = 0
D. 2x + z = 0
Trong không gian với hệ trục tọa độ Oxyz cho điểm A và đường thẳng d có phương trình x + 1 2 = y - 2 - 2 = z 1 .Phương trình đường thẳng qua điểm A,vuông góc với đường thẳng d và cắt đường thẳng d là
A. x - 2 1 = y - 1 - 3 = z - 10 - 8
B. x - 2 1 = y - 1 3 = z - 10 - 10
C. x - 1 2 = y + 1 3 = z - 3 6
D. x + 1 2 = y - 1 - 3 = z + 3 6
Phương trình mặt phẳng qua A và vuông d là 2x -2y + z -12 = 0
Khi đó và cắt nhau tại B. Đường thẳng cần tìm là đường thẳng qua hai điểm A, B có phương trình x - 2 1 = y - 1 - 3 = z - 10 - 8 .
Đáp án A.
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d có phương trình x - 1 2 = y + 2 1 = z - 3 4 . Điểm nào sau đây không thuộc đường thẳng d?
A. (1;-2;3)
B. (5;0;11)
C. (-1;3;-1)
D. (3;-1;7)
Đáp án C
Thay tọa độ điểm M trong bốn phương án vào phương trình đường thẳng d. Nhận thấy (-1;3;-1) không thuộc đường thẳng d
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1;2;3) và cho đường thẳng d có phương trình x - 2 2 = y + 2 - 1 = z - 3 1 . Tìm tọa độ của điểm B thuộc trục hoành sao cho AB vuông góc với d
A. B ( - 3 2 ; 0 ; 0 )
B. B ( 1 ; 0 ; 0 )
C. B ( 3 2 ; 0 ; 0 )
D. B ( 1 ; 0 ; 0 )
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng ∆ : x = 1 + t y = 2 - t z = 1 - 3 t . Phương trình của d là
A. x = t y = 3 t z = - t
B. x = t y = - 3 t z = - t
C. x 1 = y 3 = z - 1
D. x = 0 y = - 3 t z = t
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d : x 1 = y - 2 = z + 1 1 và d ' : x - 1 - 2 = y - 2 4 = z 2 . Viết phương trình mặt phẳn (Q) chứa hai đường thẳng d và d’.
![]()
![]()
![]()
![]()
Đáp án B.
Ta có: Hai vector chỉ phương của hai đường thẳng là cùng phương nên hai đường thẳng luôn đồng phẳng.
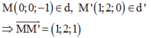
Vector chỉ phương của đường thẳng d là u → = ( 1 ; - 2 ; - 1 )
Vector pháp tuyến của mặt phẳng
![]()
Phương trình mặt phẳng
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d: x 1 = y - 2 = z + 1 1 và d'= x - 1 - 2 ) = y - 2 4 = z 2 . Viết phương trình mặt phẳng (Q) chứa hai đường thẳng d và d’
A. Không tồn tại (Q)
B. (Q): y-2z-2= 0
C. (Q): x-y-2= 0
D. (Q):-2y+4z+1= 0
Trong không gian với hệ trục tọa độ Oxyz, cho đường thẳng d: x - 1 2 = y + 1 1 = z - 3 2 và điểm A(0;-2;-2) Mặt phẳng (P) đi qua điểm A và vuông góc với đường thẳng d có phương trình là
A. 2x + y - 2z + 4 = 0
B. 2x + y + 2z - 4 = 0
C. 2x + y - 2z - 4 = 0
D. 2x + y + 2z + 4 = 0
Chọn D
Mặt phẳng (P) vuông góc với đường thẳng d nên (P) nhận vecto chỉ phương của d là một vecto pháp tuyến. Ta có phương trình mặt phẳng (P) là
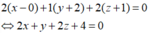
Trong không gian với hệ tọa độ Oxyz, cho d là đường thẳng đi qua gốc tọa độ O, vuông góc với trục Ox và vuông góc với đường thẳng ∆ : x = 1 + t y = 2 - t z = 1 - 3 t . Phương trình của d là.
A. x = t y = 3 t z = - t
B. x = t y = - 3 t z = - t
C. x 1 = y 3 = z - 1
D. x = 0 y = - 3 t z = t
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 , d 2 lần lượt có phương trình d 1 : x - 2 2 = y - 2 1 = z - 3 3 ; d 2 : x - 1 2 = y - 2 - 1 = z - 1 4 . Mặt phẳng cách đều hai đường thẳng có phương trình là
A. 14 x - 4 y - 8 z + 1 = 0
B. 14 x - 4 y - 8 z + 3 = 0
C. 14 x - 4 y - 8 z - 3 = 0
D. 14 x - 4 y - 8 z - 1 = 0