Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Biết rằng S A ⊥ ( A B C D ) và S B = a 3 . Tính thể tích V của khối chóp S.ABCD.
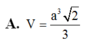
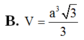
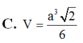
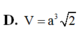
Cho hình chóp S.ABCD có đáy là hình thang vuông ở A và D, cạnh đáy AB = a, cạnh đáy CD = 2a, AD = a. Hình chiếu vuông góc của S lên đáy trùng với trung điểm CD. Biết rằng diện tích mặt bên (SBC) bằng 3 a 2 2 . Thể tích của hình chóp S.ABCD bằng:
A. a 3 B. 3 a 3 2
C. 3 a 3 D. 3 2 a 3
Chọn A.
Gọi H là trung điểm của CD, M là trung điểm của BC. Khi đó HM ⊥ BC, SM ⊥ BC. Dễ thấy tam giác HBC vuông cân ở H, do đó tính được BC, SM. Từ đó tính được SH.
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng góc giữa mặt phẳng (SAD) và đáy bằng 45 ° . Tính thể tích V của khối chóp S.ABCD
A. V = a 3 3 6
B. V = a 3 2 3
C. V = a 3 6
D. V = a 3 5 6
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, mặt bên (SAB) là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng góc giữa mặt phẳng (SAD) và đáy bằng 450. Tính thể tích V của khối chóp S.ABCD.
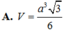
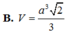
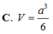
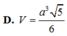
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 60 0 . Tính thể tích V của khối chóp S.ABCD.
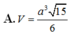
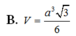
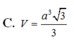
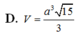
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết rằng, góc giữa mặt phẳng (SCD) và mặt phẳng đáy bằng 60 ° . Tính thể tích V của khối chóp S.ABCD.
A. V = a 3 15 6
B. V = a 3 3 6
C. V = a 3 3 3
D. V = a 3 15 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD).Biết rằng côssin của góc giữa (SCD) và (ABCD) bằng 2 19 19 . Tính a theo thể tích V của khối chóp S.ABCD
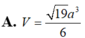
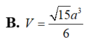
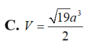
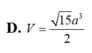
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, mặt bên SAB là tam giác cân tại S và nằm trong mặt phẳng vuông góc với (ABCD). Biết rằng côsin của góc giữa (SCD) và (ABCD) bằng 2 19 19 . Tính theo a thể tích V của khối chóp S.ABCD.
A. V = 19 a 3 6
B. V = 15 a 3 6
C. V = 19 a 3 2
D. V = 15 a 3 6
Đáp án B
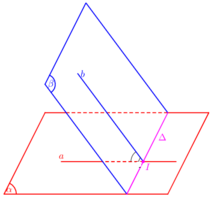
Phương pháp:
Xác định góc giữa hai mặt phẳng (α;β)
- Tìm giao tuyến Δ của (α;β)
- Xác định 1 mặt phẳng γ ⊥ Δ
- Tìm các giao tuyến a = α∩γ, b = β ∩ γ
- Góc giữa hai mặt phẳng (α;β):(α;β) = (a;b)
Cách giải:
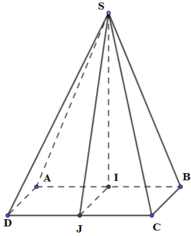
Gọi I, J lần lượt là trung điểm của AB, CD.
Tam giác SAB cân tại S ⇒ SI ⊥ AB
Vì mặt bên SAB nằm trong mặt phẳng vuông góc với (ABCD) nên SI ⊥ (ABCD)
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích cho hình chóp S.ABCD là a 3 15 6 . Góc giữa đường thẳng SC và mặt phẳng đáy(ABCD) là
A. 30°
B. 45°
C. 60°
D. 120°
Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB cân tại S và nằm trong mặt phẳng vuông góc với đáy. Biết thể tích cho hình chóp S.ABCD là a 3 15 6 Góc giữa đường thẳng SC và mặt phẳng đáy (ABCD) là
A. 30 0
B. 45 0
C. 60 0
D. 120 0
Cho hình chóp \(S.ABCD\) có đáy là hình thoi \(ABCD\) cạnh \(a\). Cho biết \(SA = a\sqrt 3 ,SA \bot AB\) và \(SA \bot A{\rm{D}}\). Tính góc giữa \(SB\) và \(C{\rm{D}}\), \(S{\rm{D}}\) và \(C{\rm{B}}\).
THAM KHẢO:

CD//AB nên góc giữa SB và CD là góc giữa AB và SB, \(\widehat{ABS}\)
CB//AD nên góc giữa SD và CB là góc giữa SD và AD, \(\widehat{ADS}\)
Ta có: tan\(\widehat{ABS}\)=tan\(\widehat{ADS}\)=\(\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
Suy ra \(\widehat{ABS}\)=\(\widehat{ADS}\)=\(\dfrac{\pi}{3}\)