Tìm số các giá trị nguyên của tham số m ∈ ( - ∞ ; + ∞ ) để hàm số y = ( 2 m - 1 ) x - ( 3 m + 2 ) cos x nghịch biến trên ℝ .
A. 3
B. 4
C. 4014
D. 218
a) Tìm tất cả các tham số m nguyên để \(F\left(x\right)=\dfrac{7}{x^2+\dfrac{1}{2}m}\) có nghiệm x nguyên và F(x) là số nguyên dương.
b) Với mọi \(m\ge0\), tìm giá trị lớn nhất của F(x).
Với mọi m < 0, tìm giá trị nhỏ nhất của F(x).
Cho hàm số y = m x + 2 2 x + m , m là tham số thực. Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để hàm số nghịch biến trên khoảng 0 ; 1 . Tìm số phần tử của S.
A. 1
B. 5
C. 2
D. 3
Tìm tất cả các giá trị nguyên của tham số m để hàm số y = x + 1 m 2 x 2 + m − 1 có bốn đường tiệm cận.
A. m<1 và m ≠ 0
B. m < 0
C. m > 1
D. m < 1
Đáp án A
Đồ thị hàm số có bốn tiệm cận ⇔ m 2 x + m − 1 = 0 có hai nghiệm
⇔ m ≠ 0 m − 1 < 0 ⇔ m < 1 ∪ m ≠ 0
a) Cho hàm số \(y=x^2+2x+3+\left|x-a+1\right|\) có bao nhiêu giá trị nguyên của tham số \(a\in\left[-10;10\right]\) sao cho giá trị nhỏ nhất của hàm số lớn hơn 2
b) Tìm tất cả các giá trị của tham số m để hệ bất pt \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\) có nghiệm
c) Gọi (x;y) là nghiệm của hệ bất pt \(\left\{{}\begin{matrix}x-2y-2\le0\\4x-3y+12\ge0\\x+3y+3\ge0\\2x+y-4\le0\end{matrix}\right.\). Tìm giá trị lớn nhất của biểu thức F=4x+5y-6
b, \(\left\{{}\begin{matrix}x^2-2x-3\le0\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-1\le x\le3\\x^2-2mx+m^2-9\ge0\end{matrix}\right.\)
Yêu cầu bài toán thỏa mãn khi phương trình \(f\left(x\right)=x^2-2mx+m^2-9\ge0\) có nghiệm \(x\in\left[-1;3\right]\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'=m^2-m^2+9=9>0,\forall m\\-1< m< 3\\f\left(-1\right)=m^2+2m-8\ge0\\f\left(3\right)=m^2-6m\ge0\end{matrix}\right.\)
\(\Leftrightarrow m\in[2;3)\cup(-1;0]\)
Tìm tất cả các giá trị nguyên của tham số m để hàm số y = m 2 x − 4 x − 1 đồng biến trên từng khoảng xác định:
A. m = 1 ; m = 2 ; m = 3
B. m = 0 ; m = − 1 ; m = − 2
C. m = − 1 ; m = 0 ; m = 1
D. m = 0 ; m = 1 ; m = 2
Đáp án C
Ta có y ' = 4 − m 2 x − 1 2 hàm số đồng biến trên tập xác định của nó
⇔ 4 − m 2 > 0 ⇔ − 2 < m < 2 do m nguyên ⇒ m = 0, m = ± 1
Tìm tổng các giá trị nguyên của tham số m để phương trình 4 sin x + 2 1 + sin x = m có tổng các nghiệm trong khoảng 0 ; π bằng π
A. 22
B. 25
C. 30
D. 33
Tìm tổng các giá trị nguyên của tham số m để phương trình 4 sin x + 2 1 + sin x = m có tổng các nghiệm trong khoảng 0 ; π bằng π .
A. 22
B. 25
C. 30
D. 33
Đáp án A
Điều kiện x ∈ ℝ
Đặt t = 2 sin x . Phương trình đã cho trở thành t 2 + 2 t = m ( * )
Vì sin x = sin α ⇔ x = α + 2 k π x = π − α + k 2 π nên để phương trình đã cho có tổng các nghiệm trong khoảng 0 ; π bằng π thì phương trình (*) phải có đúng một nghiệm t ∈ 1 ; 2 sin x ∈ 0 ; 1 thì 2 sin x ∈ 1 ; 2
Xét hàm số f t = t 2 + 2 t có bảng biến thiên
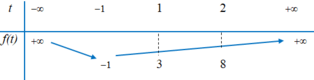
Suy ra để phương trình (*) có đúng một nghiệm t ∈ 1 ; 2 thì m ∈ 3 ; 8 .Vậy tổng các giá trị nguyên của m thỏa mãn yêu cầu bài toán là 4 + 5 + 6 + 7 = 22
Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình 2 sin 3 2 x + m sin 2 x + 2 m + 4 = 4 cos 2 2 x có nghiệm thuộc 0 ; π 6
A. 4
B. 3
C. 1
D. 6
Đáp án C
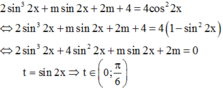
Đặt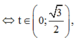
ta được
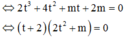
Vì 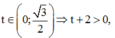
vậy
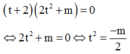
Với
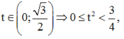
vậy để phương trình có nghiệm thì ![]()
![]()
Có 1 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Tìm số tất cả các giá trị nguyên của tham số thực m để phương trình 2 sin 3 2 x + m sin 2 x + 2 m + 4 = 4 c o s 2 2 x có nghiệm thuộc 0 ; π 6
A. 4
B. 3
C. 1
D. 6