trong mặt phẳng tọa độ Oxy có các điểm M(-2;-1), N(1,5 ; 2,5), P(-0,5 ; 0;5). chứng minh 3 điểm M, N, P thẳng hàng
VT
Những câu hỏi liên quan
Trong không gian Oxyz cho điểm M có tọa độ ( x 0 ; y 0 ; z 0 ). Tìm tọa độ hình chiếu vuông góc của điểm M trên các mặt phẳng tọa độ (Oxy), (Oyz), (Ozx).
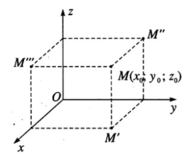
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: A = T v → ( M )
Giả sử A = (x; y). Khi đó

Vậy A = (5; 1)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho vectơ v = (2; −1) , điểm M = (3; 2). Tìm tọa độ của các điểm A sao cho: M = T v → ( A )
Giả sử A = (x; y). Khi đó

Vậy A = (1; 3)
Đúng 0
Bình luận (0)
trong mặt phẳng tọa độ Oxy cho 2 điểm B(2;2), C(0;1). Tọa độ các điểm M nằm trên trục hoành thỏa MB = 2MC
\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho 2 điểm B(2;2), C(0;1). Tọa độ các điểm M nằm trên trục hoành thỏa MB=2MC là
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB 2AM, phương trình đường phân giác trong AD : x-y 0, phương trìn đường cao CH: 2x+y+3 0. Tìm tọa độ các đỉnh A,B,C.2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC 2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y0,điểm A có hoành độ dương
Đọc tiếp
1. Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có cạnh AC đi qua điểm M (0;-1). Biết AB =2AM, phương trình đường phân giác trong AD : x-y =0, phương trìn đường cao CH: 2x+y+3 =0. Tìm tọa độ các đỉnh A,B,C.
2. Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD tâm I (-1;1). Gọi M nằm trên cạnh CD sao cho MC =2 MD. Tìm tọa độ điểm C biết đường thẳng AM có phương trình 2x-y=0,điểm A có hoành độ dương
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ điểm M’ đối xứng với điểm M qua điểm P là:
A. M’(18; 10)
B. M’(18; –10)
C. M'(9/2; 1/2)
D. M’(9; – 7)
Do điểm M’ đối xứng với điểm M qua điểm P nên P là trung điểm MM’.
Suy ra:
x P = x M + x M ' 2 y P = y M + y M ' 2 ⇔ x M ' = 2 x P − x M = 2.9 − 0 = 18 y M ' = 2 y P − y M = 2. ( − 3 ) − 4 = − 10 ⇒ M ' ( 18 ; − 10 )
Đáp án B
Đúng 0
Bình luận (0)
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình: A. y+z0 và y-z0 B. x+y0 và x-y0 C. x+z0 và x-z0 D. y+2z0 và y-2z0
Đọc tiếp
Trong không gian Oxyz, tập hợp các điểm M cách đều hai mặt phẳng tọa độ (Oxy) và (Oxz) là hai mặt phẳng có phương trình:
A. y+z=0 và y-z=0
B. x+y=0 và x-y=0
C. x+z=0 và x-z=0
D. y+2z=0 và y-2z=0
Đáp án A
Phương trình của hai mặt phẳng (Oxy) và (Oxz) lần lượt là z = 0 và y = 0.
Điểm M(x ;y ;z) cách đều hai mặt phẳng đó khi và chỉ khi
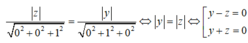
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy phép vị tự tâm I(1;2) tỉ số k = 5, biến điểm M(2;-3) thành điểm M’ có tọa độ:
A. M'(1;-5)
B.M'(8;13)
C. M'(6;-23)
D.M'(6;-27)
Phép vị tự tâm I(1; 2) tỉ số k = 5 biến điểm M(2; -3) thành điểm M’(x; y)
⇔ I M ' → = 5 I M → ⇔ x − 1 = 5 2 − 1 y − 2 = 5 − 3 − 2 ⇔ x = 6 y = − 23
Suy ra M’(6; -23).
Đáp án C
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho các điểm M(0; 4), N(–3; 2) và P(9; –3).
Tọa độ điểm I của đoạn thẳng MN là:
A. I(0; 3)
B. I(–2; 2)
C. I(-3/2;3)
D. I(–3; 3)
Tọa độ điểm I của đoạn thẳng MN là:
x I = x M + x N 2 = 0 + ( − 3 ) 2 = − 3 2 y I = y M + y N 2 = 4 + 2 2 = 3 ⇒ I − 3 2 ; 3
Đáp án C
Đúng 0
Bình luận (0)


