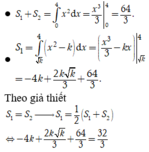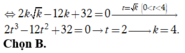Gọi (H) và (K) là hình phẳng giới hạn bởi ( E ) : x 2 16 + y 2 9 = 1 và đường x = k (k < 0). Để tỉ số thể tích khối tròn xoay tạo bởi khi quay (H) và (K) quanh Ox bằng V H V K = 5 27 thì k bằng.
A. k = -4
B. k = -3
C. k = -2
D. k = -1
Gọi (H) và (K) là hình phẳng giới hạn bởi (E) x 2 16 + y 2 9 = 1 và đường x=k (k>0). Để tỉ số thể tích khối tròn xoay tạo bởi khi quay (H) và (K) quanh Ox bằng V H V K = 5 27 thì k bằng.
A. k = -4.
B. k = -3.
C. k = -2.
D. k = -1.
Gọi (H) và (K) là hình phẳng giới hạn bởi ( E ) : x 2 16 + y 2 9 = 1 và đường x = k ( k > 0 ). Để tỉ số thể tích khối tròn xoay tạo bởi khi quay (H) và (K) quanh Ox bằng V H V K = 5 27 thì k bằng
A. k = -4
B. k = -3
C. k = -2
D. k = -1

( E ) : x 2 16 + y 2 9 = 1 ⇒ y = ± 3 4 16 - x 2
Đường thằng x = k chia elip thành hai phần (H) và (K) khi đó
V H = π ∫ - 4 k 3 14 16 - x 2 dx = 1 4 π 48 x - x 3 - 4 k = 1 4 π 48 k - k 3 + 128
V H V K = 48 k - k 3 + 128 128 - 48 k + k 3 = 5 27 ⇒ 48 k - k 3 + 128 256 = 5 32 ⇒ k 3 - 48 k - 88 = 0
với k nguyên âm k = -2
Đáp án cần chọn là C
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Đáp án A
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
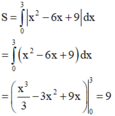
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
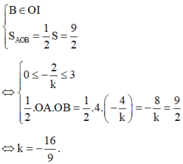 .
.
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Đáp án A
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
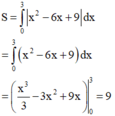
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
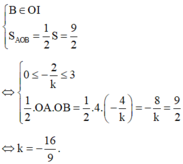
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 − 6 x + 9 và 2 đường thẳng x = 0, y = 0. Đường thẳng (d) có hệ số k ( k ∈ ℝ ) và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
A. − 16 9 .
B. 1 9 .
C. − 1 12 .
D. − 1 18 .
Đáp án A
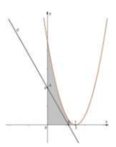
Phương trình hoành độ giao điểm của đồ thị hàm số y = x 2 − 6 x + 9 và trục hoành là:
x 2 − 6 x + 9 = 0 ⇔ x = 0 .
Diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = x 2 − 6 x + 9 và 2 đường thẳng x= 0; y = 0 là:
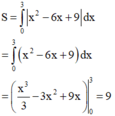
Phương trình đường thẳng (d) có hệ số góc k và cắt trục tung tại điểm A(0;4) là: y = kx +4
Gọi B là giao điểm của (d) và trục hoành ⇒ B − 4 k ; 0 .
Để (d) chia (H) thành 2 phần có diện tích bằng nhau thì:
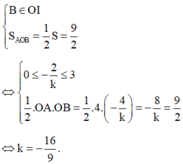
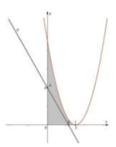
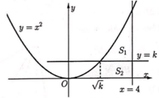
Cho hình phẳng (H) giới hạn bởi các đường y = x 2 , y = 0, x - 4. Đường thẳng y = k (0<k<16) chia hình (H) thành hai phần có diện tích S1, S2 (hình vẽ). Tìm k để S1 = S2.
A. k = 8.
B. k = 4.
C. k = 5.
D. k = 3.
Gọi (H) là hình phẳng giới hạn bởi đồ thị hàm số: y = x 2 - 6 x + 9 và 2 đường thẳng x = 0; y = 0 Đường thẳng (d) có hệ số k và cắt trục tung tại điểm A(0;4). Giá trị của k để (d) chia (H) thành 2 phần có diện tích bằng nhau là:
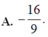
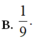
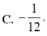
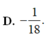
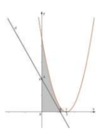

Phương trình đường thẳng(d) có hệ số góc k và cắt trục tung tại điểm A (0;4) là: y = kx +4

Đáp án A
Cho hai số thực dương a, b khác 1 và đồ thị của các hàm số y = log a x , y = log b x như hình vẽ bên. Gọi d là đường thẳng song song với trục Oy và cắt trục hoành tại điểm A có hoành độ x=k(k>1) Gọi S1 là diện tích hình phẳng giới hạn bởi y = log a x , d và trục hoành; S2 là diện tích hình phẳng giới hạn bởi y = log b x , d và trục hoành. Biết S1 = 4S2. Mệnh đề nào sau đây đúng ?
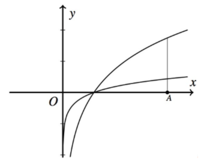
A. b = a 4
B. a = b 4
C. b = a 4 ln 2
D. a = b 4 ln 2
Theo giả thiết và công thức tích phân từng phần, ta có:
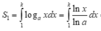
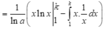
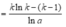
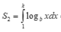
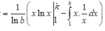
![]()
Vậy ![]()
![]()
Chọn đáp án A.
Cho hình phẳng H giới hạn bởi các đường y = x 2 , y = 0 , x = 0 , x = 4 . Đường thẳng y = k 0 < k < 16 chia hình thành hai phần có diện tích S 1 , S 2 (hình vẽ). Tìm k để S 1 = S 2
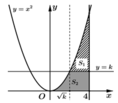
A. k = 3
B. k = 4
C. k = 5
D. k = 8
Phương trình hoành độ giao điểm: ![]()
Ta có: