Cho hàm số y = f ( x ) liên tục trên R có bảng biến thiên
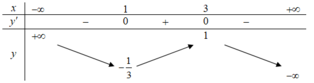
Trong các khẳng định sau, khẳng định nào là đúng?
A. Hàm số nghịch biến trên khoảng (1;3).
B. Hàm số đạt cực tiểu tại x = 3.
C. Hàm số có giá trị cực tiểu là - 1 3
D. Hàm số không có cực trị
Cho hàm số y= f( x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y= f’(x) được cho như hình vẽ dưới đây.
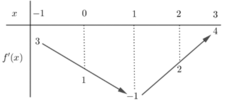
Hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng
A. (2; 4)
B. (0; 2)
C. (- 2; 0)
D.(- 4;-2)
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y=f'(x) được cho như hình vẽ bên. Hàm số y = f ( 1 - x 2 ) + x nghịch biến trên khoảng

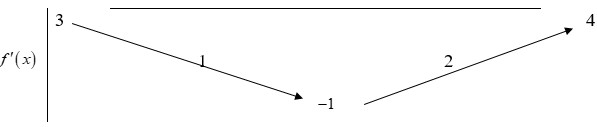
A. (-4;-2)
B. (2;4)
C. (0;2)
D. (-2;0)
Cho hàm số y = f(x) có đạo hàm liên tục trên R. Bảng biến thiên của hàm số y = f '(x) được cho như hình vẽ bên. Hàm số y = f 1 − x 2 + x nghịch biến trên khoảng
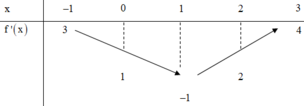
A. (2;4)
B. (-4;-2)
C. (-2;0)
D. (0;2)
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng biến thiên như sau:
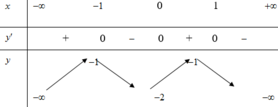
Hàm số đồng biến trên các khoảng nào
A. (0;1)
B. (-1.0)
C. (-∞;1)
D. (1;+∞)
Chọn A.
Từ bẳng biến thiên suy ra hàm số đã cho đồng biến trên các khoảng (-∞;-1) và (0;1)
Cho hàm số y = f(x) xác định, liên tục trên R và có bảng biến thiên.
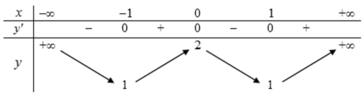
A. Hàm số đồng biến trên các khoảng (-1;0) và (1;+∞)
B. f (1) và f(-1) được gọi là giá trị cực tiểu của hàm số
C. x0 = 1 được gọi là điểm cực tiểu của hàm số
D. M(0;2) được gọi là điểm cực đại của hàm số
Đáp án D.
* Hàm số đồng biến trên (-1;0) và (1;+∞) => A đúng.
* x = -1; x = 1 là các điểm cực tiểu của hàm số, f(-1); f(1) là các giá trị cực tiểu của hàm số => B,C đúng.
* M(0;2) được gọi là điểm cực tiểu của đồ thị hàm số => D sai
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên

Khẳng định nào sai?
A. ![]() là điểm cực tiểu của hàm số.
là điểm cực tiểu của hàm số.
B. Hàm số đồng biến trên khoảng ![]() và
và ![]()
C. ![]() là điểm cực tiểu của đồ thị hàm số.
là điểm cực tiểu của đồ thị hàm số.
D. ![]() là một giá trị cực tiểu của hàm số
là một giá trị cực tiểu của hàm số
Cho hàm số y=f(x) liên tục trên R, có bảng biến thiên như hình sau:
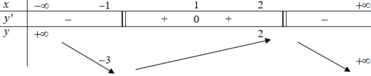
Trong mệnh đề sau, mệnh đề nào Sai?
A. Hàm số nghịch biến trên mỗi khoảng (-∞;-1), (2+∞)
B. Hàm số có hai điểm cực trị
C. Hàm số có giá trị lớn nhất bằng 2 và giá trị bé nhất bằng -3
D. Đồ thị hàm số có đúng một đường tiệm cận
Chọn đáp án D
Phương pháp
Dựa vào BBT để nhận xét các khoảng đồng biến, nghịch biến của hàm số.
Cách giải
Dựa vào BBT ta thấy hàm số đồng biến trên (-1;2) và nghịch biến trên các khoảng (-∞;-1) và (2;+∞).
⇒ đáp án A đúng.
Hàm số có hai điểm cực trị là
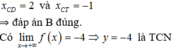
Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng biến thiên như hình bên dưới. Hàm số đã cho đồng biến trên khoảng nào dưới đây?

A. (1;+∞)
B.(-1;0)
C. (-∞;1)
D.(0;1)
Chọn đáp án D
Phương pháp
Sử dụng cách đọc bảng biến thiên để suy ra khoảng đồng biến của hàm số.
Hàm số liên tục trên (a;b) có y’>0 với x thuộc (a;b) thì hàm số đồng biến trên (a;b).
Cách giải
Từ BBT ta có hàm số đồng biến trên các khoảng (-∞;-1) và (0;1).
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như sau:
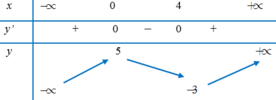
Hàm số đạt cực đại tại điểm nào trong các điểm dưới đây?
A. x = -3
B. x = 5
C. x = 4
D. x = 0
Đáp án D.
Từ bảng biến thiên của hàm số ta có hàm số đạt cực đại tại x = 0 , y C D = 5 ; hàm số đạt cực tiểu tại x = 4 , y C T = − 3. Do đó phương án đúng là D.
Phân tích phương án nhiễu.
Phương án A: Sai do HS nhầm với giá trị cực tiểu của hàm số.
Phương án B: Sai do HS nhầm với giá trị cực đại của hàm số.
Phương án C: Sai do HS nhầm với điểm cực tiểu của hàm số.