Phương trình cos x = 3 2 có nghiệm thỏa mãn 0 ≤ x ≤ π là:
A. x = π 3 + k 2 π
B. x = π 6 + k 2 π
C. x = π 3
D. x = π 6
Đáp án D
Ta có: ⇔ c o s x = 3 2 ⇔ x = ± π 6 + k 2 π , k ∈ ℤ . Vì 0 ≤ x ≤ π nên x = π 6 .
Nghiệm của phương trình cos2 x- cosx = 0 thỏa mãn điều kiện 0 < x < π
A. x= π / 6
B. x= π / 2
C. x= π / 4
D. x=- π / 2
Hướng dẫn giải
Chọn B.
Ta có : cos2 x- cosx = 0 ó cosx. ( cosx – 1) = 0
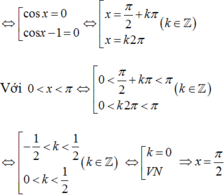
Nghiệm của phương trình cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π là
A. x = π 2
B. x = - π 2
C. x = π 6
D. x = π 4
Tìm nghiệm của phương trình lượng giác cos 2 x − cos x = 0 thỏa mãn điều kiện 0 < x < π
A. x = π 2
B. x = 0
C. x = π
D. x = 2
Đáp án A
Phương pháp: Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
Cách giải:
cos 2 x − cos x = 0
⇔ cos x cos x − 1 = 0
⇔ cos x = 0 cos x = 1
⇔ x = π 2 + k π x = 2 k π , k ∈ ℤ
+) Với: x = π 2 + k π : 0 < x < π ⇔ 0 < π 2 + k π < π ⇔ − π 2 < k 2 π < π 2 ⇔ − 1 4 < k < 1 4
Mà k ∈ ℤ nên k = 0 khi đó ta có x = π 2
+) Với: x = 2 k π : 0 < x < π ⇔ 0 < 2 k π < π ⇔ 0 < k < 1 2
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.
Nghiệm của phương trình lượng giác cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π là
A. 0
B. 3 π 4
C. π 2
D. - π 2
Nghiệm của phương trình lượng giác cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π là
A. x = 0
B. x = 3 π 4
C. x = π 2
D. x = - π 2
1Tìm m để phương trình mcos²x - msin2x - msin²x=0 để phương trình có nghiệm.
2 Tìm x € (0; π/2) thỏa mãn pt cos5x.sin4x = cos3x.sin2x
1,
Nếu m = 0, phương trình có tập nghiệm là S = R, thỏa mãn yêu cầu bài toán
Nếu m ≠ 0 phương trình tương đương
cos2x - sin2x - sin2x = 0 ⇔ cos2x = sin2x, luôn có nghiệm trên R
Vậy m nào cũng sẽ thỏa mãn ycbt
Phương trình sin 2 x = - 1 2 có bao nhiêu nghiệm thỏa mãn 0 < x < π
A. 1
B. 3
C. 2
D. 4
Có bao nhiêu nghiệm của phương trình sin 2 x - sin x = 0 thỏa mãn điều kiện 0 < x < π
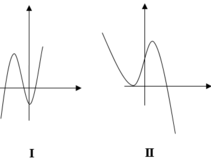
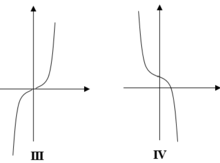
A. Đồ thị (III) xảy ra khi
B. Đồ thị (IV) xảy ra khi
C. Đồ thị (II) xảy ra khi
D. Đồ thị (I) xảy ra khi
