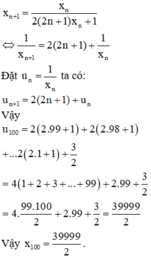Cho dãy số u n , n ∈ ℕ * xác định bởi u 1 = 2 u n + 1 + 4 u n = 4 - 5 n . Tổng S = u 2018 - 2 u 2017 bằng
A. S = 2015 - 3 . 4 2017
B. S = 201 - 3 . 4 2018
C. S = 2016 + 3 . 4 2018
D. S = 2015 + 3 . 4 2017
Cho dãy số u ( n ) xác định bởi u ( 1 ) = 1 ; u ( m + n ) = u ( m ) + u ( n ) + m n , ∀ m , n ∈ ℕ * . Tính u ( 2017 )
A. 2035153
B. 2035154
C. 2035155
D. 2035156
Chọn A
Phương pháp: Tìm công thức số hạng tổng quát
Cách giải: Ta có:
u ( 1 ) = 1
u ( 2 ) = u ( 1 ) + u ( 1 ) = 2 u ( 1 ) + 1
u ( 3 ) = u ( 2 ) + u ( 1 ) = 3 u ( 1 ) + 1 + 2
u ( 4 ) = u ( 3 ) + u ( 1 ) = 4 u ( 1 ) + 1 + 2 + 3
. . .
u ( 2017 ) = u ( 2016 ) + u ( 1 ) = 2017 u ( 1 ) + 1 + 2 + 3 . . . + 2016
⇒ u ( 2017 ) = 1 + 2 + 3 . . . + 2016 + 2017 = 2035153
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = u n 2 + 2 u n + 2019 , n ≥ 2 , n ∈ ℕ Tính l i m u n + 1 u n
A. 1
B. + ∞
C. 2018
D . 2017 2018
Cho dãy số xác định bởi u 1 = 1 ; u n + 1 = 1 3 2 u n + n − 1 n 2 + 3 n + 2 ; n ∈ ℕ * . Khi đó u 2018 bằng
A. u 2018 = 2 2016 3 2017 + 1 2019 .
B. u 2018 = 2 2018 3 2017 + 1 2019 .
C. u 2018 = 2 2017 3 2018 + 1 2019 .
D. u 2018 = 2 2017 3 2018 + 1 2019 .
Đáp án A.
Ta có
n − 1 n 2 + 3 n + 2 = n − 1 n + 1 n + 2 = A n + 1 + B n + 2 ⇒ A + B = 1 2 A + B = − 1 ⇔ A = − 2 B = 3 .
Lại có 3 u n + 1 = 2 u n − 2 n + 1 + 3 n + 2
⇔ 3 u n + 1 − 1 n + 2 = 2 u n − 1 n + 1 .
Đặt v n = u n − 1 n + 1 ⇒ v 1 = 1 2
và v n = u n − 1 n + 1 → v n
là cấp số nhân với v 1 = 1 2 ; q = 1 3
⇒ v n = 1 2 . 2 3 n − 1 = 3 4 . 2 3 n → u n = v n + 1 n + 1 = 3 4 . 2 3 n + 1 n + 1 = 2 n − 2 3 n − 1 + 1 n + 1 .
⇒ u 2018 = 2 n − 2 3 n − 1 + 1 n + 1 n = 2018 = 2 2016 3 2017 + 1 2019 .
Cho dãy số ( u n ) xác định bởi u n = 1 n 2 + 3 n 2 + . . . + 2 n - 1 n 2 , n ∈ ℕ * . Giá trị của l i m u n bằng
A. 0.
B. + ∞ .
C. - ∞ .
D. 1
Chọn D
Ta có u n = 1 n 2 + 3 n 2 + . . . + 2 n - 1 n 2
n 1 + 2 n - 1 2 n 2 = 1
Vậy l i m u 1 = l i m 1 = 1
Cho dãy số u n xác định bởi u 1 = 1 u n + 1 = u n + n 3 , ∀ n ∈ ℕ * . Tìm số nguyên dương n nhỏ nhất sao cho u n − 1 ≥ 2039190 ?
A. n = 2017.
B. n = 2020.
C. N = 2018.
D. N = 2019.
Đáp án B.
Ta có u n = u n − 1 + n − 1 3 ⇔ u n − u n − 1 = n − 1 3 ⇒ u n − 1 − u n − 2 = n − 2 3 .
Tương tự, ta được u 2 − u 1 = 1 3 . Cộng trừ 2 vế suy ra u n − u 1 = 1 3 + 2 3 + ... + n − 1 3
⇔ u n − 1 = n n − 1 2 2 ⇒ u n − 1 = n n − 1 2 ≥ 2039190 ⇔ n ≥ 2020.
Cho dãy số u n xác định bởi u n = 1 n 2 + 3 n 2 + . . . + 2 n - 1 n 2 , n ∈ ℕ * . Giá trị của l i m u n bằng
A. 0
B. -1
C. 2
D. 1
Xét dãy số ( u n ) , n ∈ ℕ * được xác định bởi hệ thức u 1 = 2 u n + 1 = 2 u n - n + 1 .Tìm u 10
A. u 10 = 1024
B. u 10 = 1014
C. u 10 = 1034
D. u 10 = 1025
Đáp án C
Đặt v n = u n - n ( n ∈ N * )
Chia ra được u n = 2 n + n
Cho dãy số u n xác định bởi u 1 = 1 và u n + 1 = u 2 n + 2 , ∀ n ∈ ℕ * . Tổng S = u 1 2 + u 2 2 + u 3 2 + . . . + u 1001 2 bằng:
A. 1002001
B. 1001001
C. 1001002
D. 1002002
Cho dãy số x n xác định bởi x 1 = 2 3 và x n + 1 = x n 2 2 n + 1 x n + 1 , ∀ n ∈ ℕ * . Mệnh đề nào dưới đây là đúng?
A. x 100 = 2 39999
B. x 100 = 39999 2
C. x 100 = 2 40001
D. x 100 = 2 40003
Chọn B.
Phương pháp:
Cách giải: Ta có: