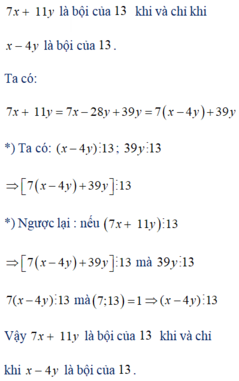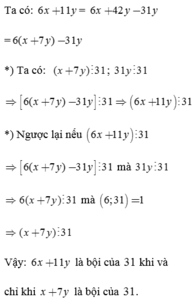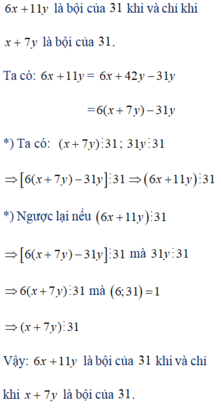Cho x, y thuộc Z. Chứng minh rằng 7x + 11y là bội của 13 khi và chỉ khi x – 4y là bội của 13.
PB
Những câu hỏi liên quan
Cho x, y thuộc Z. Chứng minh rằng 7x + 11y là bội của 13 khi và chỉ khi x - 4y là bội của 13
Cho x,y,z ∈ Z.Chứng minh rằng:
a, 6x + 11y là bội của 31 khi và chỉ khi x + 7y là bội của 31
b, 7x + 11y là bội của 13 khi và chỉ khi x - 4y là bội của 13
giúp nhé☺️
Cho x, y thuộc Z. Chứng minh rằng 6x + 11y là bội của 31 khi và chỉ khi x + 7y là bội của 31.
Cho x, y thuộc Z. Chứng minh rằng
6x + 11y là bội của 31 khi và chỉ khi x + 7y là bội của 31
Cho x,y thuộc Z. Chứng minh rằng 6x + 11y là bội của 31 và khi và chỉ khi x + 7y là bội của 31
Shizuka Chan
Ta biến đổi : k nha :)
(6x+11y) =31(x+6y)-25(x+7y)
Do 6x+11y và 31(x+6y) chia hết cho 31
=> 25(x+7y) chia hết cho 31
Do (25,31)=1 (2 số nguyên tố cùng nhau)
=> x+7y chia hết cho 31
Đúng 0
Bình luận (0)
Cho x, y thuộc Z.Chứng minh rằng 6x + 11y là bội của 31 và khi và chỉ khi x + 7y là bội của 31
Có: 6x+11y⋮31⇒6(6x+11y)⋮316x+11y⋮31⇒6(6x+11y)⋮31
⇒36x+66y⋮31⇒31x+31y+5x+35y⋮31⇒36x+66y⋮31⇒31x+31y+5x+35y⋮31
⇒31(x+y)+5(x+7y)⇒31(x+y)+5(x+7y)
⇒31(x+y)⋮31⇒5(x+7y)⋮31⇒31(x+y)⋮31⇒5(x+7y)⋮31
Mà ƯCLN (5,31) = 1
Vậy: x + 7y chia hết cho 31
Vậy x + 7y là bội 31
CHÚC HỌC GIỎI
cho x,y thuộc Z :7.x là bội của 13 khi và chỉ khi x-4.y là bội của 13
Cho x,y là các số nguyên. Chứng minh rằng ( 6x+11y) là bội của 31 khi và chỉ khi ( x +7y) là bội của 31.
Nguyễn Linh Chi Vâng ạ, vậy e thử làm cách này, sẽ giải quyết được cả hai chiều, mong cô xem hộ em ạ :
Đặt \(A=6x+11y\), \(B=x+7y\)
Ta có : \(5A+B=5\left(6x+11y\right)+\left(x+7y\right)=31x+62y\)
Rõ ràng thấy, \(5A+B⋮13\forall x,y\inℤ\). Do đó :
+) Nếu \(A⋮31\)thì \(5A⋮31\) \(\Rightarrow B⋮31\)
+) Nếu \(B⋮31\) thì \(5A⋮31\) mà \(\left(5,31\right)=1\) nên \(A⋮31\)
Vậy : bài toán được chứng minh !!
Ta có : \(6x+11y=31\left(x+6y\right)-25\left(x+7y\right)\)
Mà : \(31\left(x+6y\right)⋮31\)
\(\Rightarrow25\left(x+7y\right)⋮31\), (25,31)=1
\(\Rightarrow x+7y⋮31\left(đpcm\right)\)
Đạt ơi! Bài này là hai chiều
Em phải chứng minh hai bài toán:
+) Chứng minh rằng : ( 6x + 11y) là bội của 31 thì ( x + 7y) là bội của 31
+) Chứng minh rằng: ( x + 7y) là bội của 31 thì ( 6x + 11 y ) là bội của 31
Cho x, y thuộc Z. Chứng minh rằng: 5x + 47y là bội của 17 khi và chỉ khi x + 6y là bội của 17.
5x + 47y (1)
= 5x + 30y + 17y = 5(x+6y) + 17y.
17y luôn chia hết cho 17. Vậy để (1) chia hết cho 17 <=> x + 6y chia hết 17
Đúng 0
Bình luận (0)
giải cho hẳn hoi thế này bố ai mà hiểu
Đúng 1
Bình luận (0)
Ta có :5x+47y = 5x+30y+17y
=5x+5.6.y+17y
=5(x+6y)+17y
Vì 17y chia hết cho 17 => 5.(x+6y) chia hết cho 17
Mà 5 ko chia hết cho 17 =>muốn 5.(x+6y) chia hết cho 17 thì x+6y phải chia hêt cho 17