Chứng minh rằng, với a>b>0 thì a - b < a - b
PB
Những câu hỏi liên quan
Chứng minh rằng, với a>b>0 thì a - b < a - b
Với a>b>0 để chứng minh a - b < a - b
ra quy về so sánh a v ớ i a - b + b
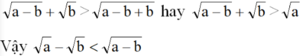
Đúng 0
Bình luận (0)
a) So sánh .. 25 - 16 v à 25 - 16
b) Chứng minh rằng với a>b>0 thì
... a - b < a - b
![]()
√25 - √16 = √52 - √42 = 5 - 4 = 1
Vì 3 > 1 nên

(Lưu ý: Ở phần giải trên có sử dụng kết quả của phần b) Bài 26 (trang 16 SGK Toán 9 Tập 1), trong đó áp dụng cho hai số là (a - b) và b.)
Đúng 0
Bình luận (0)
chứng minh rằng,với hai số a,b thỏa mãn a>b>0 thì \(\sqrt{a}\)-\(\sqrt{b}\)<\(\sqrt{a-b}\)
chứng minh rằng,với hai số a,b thỏa mãn a>b>0 thì \(\sqrt{a}-\sqrt{b}\)<\(\sqrt{a-b}\)
\(\sqrt[]{a}-\sqrt[]{b}< \sqrt[]{a-b}\left(a>b>0\right)\)
\(\Leftrightarrow\left(\sqrt[]{a}-\sqrt[]{b}\right)^2< \left(\sqrt[]{a-b}\right)^2\)
\(\Leftrightarrow a+b-2\sqrt[]{ab}< a-b\)
\(\Leftrightarrow2\sqrt[]{ab}-2b>0\)
\(\Leftrightarrow2\sqrt[]{b}\left(\sqrt[]{a}-\sqrt[]{b}\right)>0\left(1\right)\)
mà \(a>b>0\)
Nên \(\left(1\right)\) luôn luôn đúng
Vậy \(\sqrt[]{a}-\sqrt[]{b}< \sqrt[]{a-b}\)
Đúng 2
Bình luận (0)
Chứng minh rằng nếu (a+2002):(a-2002)=(b+2001):(b-2001) với a#0;b#0;b3+-2001 thì a:2002=b:2001
a) Chứng minh rằng,với a>b>0 thì căn a-căn b<căn a-b
Bài 4: Chứng minh rằng: -(a-b-c)+(-a+b-c)-(-a+b+c)=-(a-b+c)
Bài 5: Cho M=(-a+b)-(b+c-a)+(c-a) Chứng minh rằng: Nếu a<0 thì M>0
Mình cần gấp ạ!
\(4,VT=-a+b+c-a+b-c+a-b-c=-a+b-c=-\left(a-b+c\right)=VP\\ 5,M=-a+b-b-c+a+c-a=-a\\ M>0\Rightarrow-a>0\Rightarrow a< 0\)
Đúng 5
Bình luận (0)
chứng minh rằng nếu a+b/c+d=b+c/d+a với a+b+c+d khác 0 thì a=c
\(\frac{a+b}{c+d}=\frac{b+c}{d+a}\)
<=>\(\frac{a+b}{c+d}+1=\frac{b+c}{d+a}+1\)
<=> \(\frac{a+b+c+d}{c+d}=\frac{a+b+c+d}{d+a}\)
<=> \(\frac{a+b+c+d}{c+d}-\frac{a+b+c+d}{d+a}=0\)
<=> \(\left(a+b+c+d\right)\left(\frac{1}{c+d}-\frac{1}{d+a}\right)=0\)
<=> \(\orbr{\begin{cases}a+b+c+d=0\\\frac{1}{c+d}-\frac{1}{d+a}=0\end{cases}\Leftrightarrow\orbr{\begin{cases}a+b+c+d=0\\c=a\end{cases}\left(đpcm\right)}}\)
Đúng 1
Bình luận (0)
Chứng minh rằng nếu a + b/ b+ c = c+ d/ d+ a thì a= c hoặc a+ b+ c+ d= 0 (với c+ d# 0)Cho x/a+2b+c= y/2a+y-z = z/4a-4b+c. Chứng minh rằng : a/x+2y+z=b/ 2x+y-z = c/ 4x- 4y+ c
Xem chi tiết
( với abc # 0 và các mẫu đều khác 0)





