Trong không gian tọa độ Oxyz, cho các điểm A (1;2;3), B (2;1;0), C (4;3;-2), D (3;4;1), E (1;1;-1). Hỏi có bao nhiêu mặt phẳng cách đều 5 điểm trên?
A. 1
B. 4.
C. 5
D. Không tồn tại.
Trong không gian với hệ trục tọa độ Oxyz, cho các điểm A(-1;2;-3); B(2; -1; 0). Tọa độ của vectơ A B → là
A. A B → = 1 ; - 1 ; 1
B. A B → = 1 ; 1 ; - 3
C. A B → = 3 ; - 3 ; 3
D. A B → = 3 ; - 3 ; - 3
Trong không gian Oxyz, cho các điểm A ( 2 ; - 2 ; 1 ) , B ( 1 ; - 1 ; 3 ) . Tọa độ của vectơ A B → là
A. (1;-1;-2)
B. (-1;1;2)
C. (3;-3;4)
D. (-3;3;-4)
Trong không gian Oxyz, cho các điểm A(2;-2;1), B(1;-1;3). Tọa độ của véctơ A B → là
A. (1 ;-1 ;-2)
B. (-1 ;1 ;2)
C. (3 ;-3 ;4)
D. (-3 ;3 ;-4)
Trong không gian Oxyz, cho các điểm A(2;-2;1), B(1;-1;3). Tọa độ của vecto A B → là:
![]()
![]()
![]()
![]()
Đáp án A.
Phương pháp:
+) Cho hai điểm ![]()
Khi đó ta có: ![]()
Cách giải:
Ta có:
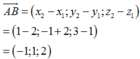
#2H3Y1-1~Trong không gian với hệ tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với điểm A qua gốc tọa độ O là:
A. A'(3;-2;1)
B. A'(3;2;-1)
C. A'(3;-2;-1)
D. A'(3;2;1).
Đáp án A
Ta có xA' = 2xO-xA = 3; yA' = 2yO-yA = -2; zA' = 2zO-zA=1. Vậy A'(3;-2;1).
Trong không gian với hệ trục tọa độ Oxyz, cho hình hộp A B C D . A ' B ' C ' D ' có tọa độ các điểm A 1 ; 2 ; - 1 , C 3 ; - 4 ; 1 , D ' 0 ; 3 ; 5 . Giả sử tọa độ điểm A'(x;y;z) thì x + y + z bằng
A. 2
B. -3
C. 7
D. 5
Trong không gian với hệ tọa độ Oxyz cho điểm Phương trình mặt phẳng ( Q ) đi qua các hình chiếu của điểm A lên các trục tọa độ là
A . ( Q ) : x - y + 2 z - 2 = 0
B . ( Q ) : 2 x - 2 y + z - 2 = 0
C . ( Q ) : x - 1 + y 1 + z - 2 = 1
D . ( Q ) : x - y + 2 z + 6 = 0
Chọn B.
Gọi B, C, D lần lượt là hình chiếu của A lên các trục Ox , Oy , Oz ⇒ B ( 1 ; 0 ; 0 ) C ( 0 ; - 1 ; 0 ) D ( 0 ; 0 ; 2 )
Suy ra phương trình mặt phẳng ( Q ) : x 1 + y - 1 + z 2 = 1 ⇔ 2 x - y + z - 2 = 0 .
Trong không gian với hệ tọa độ Oxyz, cho các điểm A ( 2 ; 1 ; - 1 ) , B ( 3 ; 3 ; 1 ) , C ( 4 ; 5 ; 3 ) . Khẳng định nào đúng?
A. AB ⊥ AC
B. A, B, C thẳng hàng.
C. AB = AC
D. O, A, B, C là 4 đỉnh của một hình tứ diện.
Đáp án B
Phương pháp :
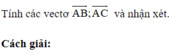
A
(
2
;
1
;
-
1
)
,
B
(
3
;
3
;
1
)
,
C
(
4
;
5
;
3
)
.
![]()
=> A, B, C thẳng hàng.
Trong không gian với hệ tọa độ Oxyz, cho các điểm A(2;1;-1), B(3;3;1), C(4;5;3) . Khẳng định nào đúng?
A. AB ⊥ AC
B. A,B,C thẳng hàng
C. AB=AC
D. O, A, B, C là bốn đỉnh của một hình tứ diện
Trong không gian với hệ trục tọa độ Oxyz, cho điểm A(-3;2;-1). Tọa độ điểm A' đối xứng với A qua trục Oy là
A. A'(-3;2;1)
B. A'(3;2;-1)
C. A'(3;2;1)
D. A'(3;-2;-1)