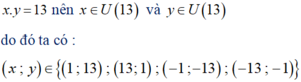Tìm các số nguyên x, y sao cho (x - 13).(y + 2) = 13
PB
Những câu hỏi liên quan
Tìm các số nguyên x,y sao cho: (x-13).(y+2)=13
Vì \(x,y\inℤ\) và \(\left(x-13\right)\cdot\left(y+2\right)=13\Rightarrow y+2\inƯ\left(13\right)=\left\{\pm1;\pm13\right\}\)
| y+2 | 1 | -1 | 13 | -13 |
x-13 | 13 | -13 | 1 | -1 |
| y | -1 | -3 | 11 | -15 |
| x | 26 | 12 | 14 | -12 |
(x-13).(y+2)=13
=> (y+2)\(\in\)Ư(13)={1;13; -13; -1}
Nếu y+2= 1 => x= 1-2 => y= -1
Nếu y+2=13 => y= 13-2 => y= 11
Nếu y+2= -1 => y= -1-2 => y= -3
Nếu y+2 = -13 => y= -13-2 => y= -15
Sau đó bn thay vào r tự tìm nha
tìm các cặp số nguyên dương x,y sao cho x^2 +x+13=y
Tìm các số nguyên dương x,y sao cho x2+y2-13.(x-y)=0
Tìm các số nguyên x, y sao cho
a) x.y = 13
b)x.y = 8 và x < y
a) x . y = 13 nên x ∈ U 13 và y ∈ U 13 do đó ta có x ; y ∈ 1 ; 13 ; 1 3 ; 1 ; − 1 ; − 13 ; − 13 ; − 1
b) x . y = 8 và x < y ; x ∈ U 8 ; y ∈ U 8 do đó ta có x ; y ∈ − 8 ; − 1 ; − 4 ; − 2 ; 1 ; 8 ; 2 ; 4
Đúng 0
Bình luận (0)
Tìm các số nguyên x , y sao cho
a) x . y = 13
b) x . y = 8 và x < y
a) x . y = 13 nên x ∈ U 13 và y ∈ U 13 do đó ta có x ; y ∈ 1 ; 13 ; 1 3 ; 1 ; − 1 ; − 13 ; − 13 ; − 1
b) x . y = 8 v à x < y , x ∈ U 8 , y ∈ U 8 do đó ta có x ; y ∈ − 8 ; − 1 ; − 4 ; − 2 ; 1 ; 8 ; 2 ; 4
Đúng 0
Bình luận (0)
Tìm các số nguyên x, y sao cho x.y = 13
Tìm các số nguyên x, y sao cho x.y = 13
Tìm các giá trị \(x,y\) nguyên dương sao cho: \(x^2=y^2+2y+13\)
\(x^2=\left(y+1\right)^2+12\)
\(\Leftrightarrow\left(x-y-1\right)\left(x+y+1\right)=12\)
Do \(x,y\in N\)* nên \(x-y-1;x+y+1\inƯ\left(12\right)\) và \(x+y+1\ge1+1+1=3\)
TH1: \(x+y+1=12\Rightarrow x-y-1=1\)
\(\Leftrightarrow x=\dfrac{13}{2};y=\dfrac{9}{2}\) (ktm)
TH2:\(x+y+1=6;x-y-1=2\)
\(\Leftrightarrow x=4;y=1\) (thỏa mãn)
TH3: \(x+y+1=4;x-y-1=3\)
\(\Leftrightarrow x=\dfrac{7}{2};y=-\dfrac{1}{2}\) (ktm)
TH4: \(x+y+1=3;x-y-1=4\) (ktm)
Vậy \(x=4;y=1\)
Đúng 1
Bình luận (0)
\(x^2=y^2+2y+13\)
\(\Leftrightarrow x^2=y^2+2y+1+12\)
\(\Leftrightarrow x^2=\left(y+1\right)^2+12\)
\(\Leftrightarrow x^2-\left(y+1\right)^2=12\)
\(\Leftrightarrow\left(x-y-1\right)\left(x+y+1\right)=12\)
Vi x;y nguyên dương
\(\Rightarrow\left(x-y-1\right);\left(x+y+1\right)\in B\left(12\right)=\left\{1;2;3;4;6;12\right\}\left(x-y-1< x+y+1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}x+y+1\in\left\{12;6;4\right\}\\x-y-1\in\left\{1;2;3\right\}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x\in\left\{\dfrac{13}{2};4;\dfrac{7}{2}\right\}\\y\in\left\{\dfrac{9}{2};1;-\dfrac{1}{2}\right\}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\) (x;y nguyên dương)
Vậy \(\left(x;y\right)\in\left(4;1\right)\) thỏa mãn đề bài
Đúng 0
Bình luận (0)
Câu 1: Cho 13 số nguyên, trong đó tổng của bốn số bất kì trong 13 số ấy là một số nguyên dương. Chứng tỏ tổng của 13 số ấy là một số nguyên dương.
Câu 2: Tìm các số nguyên tố x, y sao cho x2 + 45 = y2.
2,
-Ta có: \(x^2+45=y^2\)
\(\Leftrightarrow y^2>45\Rightarrow y\) là số ng tố lẻ
\(\Rightarrow x^2\)chẵn( vì: chẵn +5=lẻ)
\(\Rightarrow x=2\)
\(\Leftrightarrow2^2+45=y\)
\(\Leftrightarrow y=\pm\sqrt{49}=\pm7\)
-Mà: snt>0
-Vậy: \(x=2;y=7\)
Đúng 0
Bình luận (0)