Giá trị của tan(π/4) là
A. 1
B. 2 2
C. - 2 2
D. -1
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
PB
Những câu hỏi liên quan
Cho a, b là các số thực thuộc khoảng
(
0
;
π
/
2
)
và thỏa mãn điều kiện cota-tan(
π
/
2
-b)a-b. Tính giá trị của biểu thức
P
3
a
+
7
b
a
+
b
A. P5 B. P2 C. P4 D. P6
Đọc tiếp
Cho a, b là các số thực thuộc khoảng ( 0 ; π / 2 ) và thỏa mãn điều kiện cota-tan( π / 2 -b)=a-b. Tính giá trị của biểu thức P = 3 a + 7 b a + b
A. P=5
B. P=2
C. P=4
D. P=6
Biết sina = -4/5 với 3π/4 < a < π. Giá trị tan a là
A. 1/2 B. 2
C. -2 D. -1/2
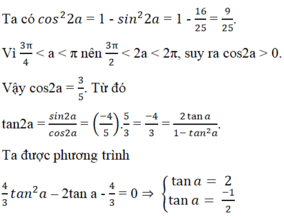
Vì 3π/4 < a < π nên tan a < 0. Vậy tan a = (-1)/2. Đáp án là D.
Đúng 0
Bình luận (0)
Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π/2) là:
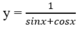
A. 1 B. 2 2
C. - 2 D. 2/ 2
Đáp án: D.
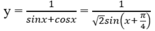
Trên khoảng (0; π/2), sin(x + π/4) ≤ 1;
Dấu "=" xảy ra ⇔ x = π/4
Suy ra giá trị nhỏ nhất của hàm số là min y = y(π/4) = 2 /2.
Đúng 0
Bình luận (0)
Giá trị nhỏ nhất của hàm số sau trên khoảng (0;
π
/2) là:
y
1
sinx
+
cosx
A. 1 B. 2
2
C. -
2
D.
2
/2
Đọc tiếp
Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π /2) là:
y = 1 sinx + cosx
A. 1 B. 2 2
C. - 2 D. 2 /2
Đáp án: D.
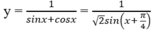
Trên khoảng (0; π /2), sin(x + π /4) ≤ 1;
Dấu "=" xảy ra ⇔ x = π /4
Suy ra giá trị nhỏ nhất của hàm số là min y = y( π /4) = 2 /2.
Đúng 0
Bình luận (0)
Cho π/2 < a < 3π/4. Giá trị tan2a là
A. -2 7 B. 3 3 /4
C. -3 7 D. 3 7
Với π/2 < a < 3π/4 thì cosa < 0. Ta có
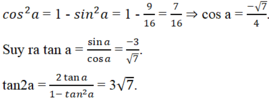
Đáp án là D.
Đúng 0
Bình luận (0)
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi , f50 hz vào 2 đầu đoạn mạch gồm điện trở thuần R , cuộn thuần cảm có L thay đổi được , tụ điện có C 10^{-4}/ π F . Khi LL1 2/ π H thì iI_{1}sqrt{2}Cos(100 π- π/12) . Khi LL24/π thì iI_{2}sqrt{2}Cos(100 π- π/4) . Giá trị của R là A.100sqrt{3} B.100C.100sqrt{2}D.200
Đọc tiếp
Đặt điện áp xoay chiều có giá trị hiệu dụng U không đổi , f=50 hz vào 2 đầu đoạn mạch gồm điện trở thuần R , cuộn thuần cảm có L thay đổi được , tụ điện có C = \(10^{-4}/ π \) F . Khi L=L1 = \(2/ π \) H thì i=\(I_{1}\sqrt{2}Cos(100 π- π/12)\) . Khi L=L2=4/π thì i=\(I_{2}\sqrt{2}Cos(100 π- π/4)\) . Giá trị của R là
A.\(100\sqrt{3}\)
B.100
C.\(100\sqrt{2}\)
D.200
Hình bên minh họa : hình gồm một nửa hình cầu và một hình nón.Thể tích của hình nhận giá trị nào sau đây?A. (2/3).
π
x
3
(
c
m
3
)B.
π
.x3
x
3
(
c
m
3
)C. (4/3).
π
....
Đọc tiếp
Hình bên minh họa : hình gồm một nửa hình cầu và một hình nón.Thể tích của hình nhận giá trị nào sau đây?
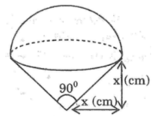
A. (2/3). π x 3 ( c m 3 )
B. π .x3 x 3 ( c m 3 )
C. (4/3). π . x 3 ( c m 3 )
D. 2 π . x 3 ( c m 3 )
Thể tích nửa hình cầu là: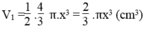 
Thể tích hình nón là :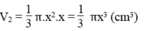 
Tổng thể tích của hai hình: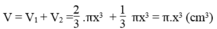 
Vậy chọn đáp án B
Đúng 0
Bình luận (0)
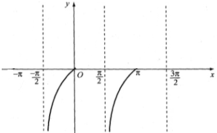
Hãy xác định giá trị của x trên đoạn [- π ; 3π/2] để hàm số y = tan x:
a. Nhận giá trị bằng 0
b. Nhận giá trị bằng 1
c. Nhận giá trị dương
d. Nhận giá trị âm
Quan sát đồ thị hàm số y = tan x trên đoạn [-π; 3π/2].
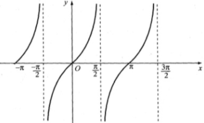
a. tan x = 0 tại các giá trị x = -π; 0; π.
(Các điểm trục hoành cắt đồ thị hàm số y = tanx).
b. tan x = 1 tại các giá trị x = -3π/4; π/4; 5π/4.
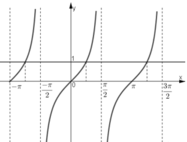
c. tan x > 0 với x ∈ (-π; -π/2) ∪ (0; π/2) ∪ (π; 3π/2).
(Quan sát hình dưới)
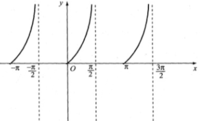
d. tan x < 0 khi x ∈ [-π/2; 0) ∪ [π/2; π)
(Quan sát hình dưới).
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:a) f(x)
(
25
-
x
2
)
trên đoạn [-4; 4]b) f(x) |
x
2
– 3x + 2| trên đoạn [-10; 10]c) f(x) 1/sinx trên đoạn [π/3; 5π/6]d) f(x) 2sinx + sin2x trên đoạn [0; 3π/2]
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau:
a) f(x) = ( 25 - x 2 ) trên đoạn [-4; 4]
b) f(x) = | x 2 – 3x + 2| trên đoạn [-10; 10]
c) f(x) = 1/sinx trên đoạn [π/3; 5π/6]
d) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
a) 
f′(x) > 0 trên khoảng (-4; 0) và f’(x) < 0 trên khoảng (0; 4).
Hàm số đạt cực đại tại x = 0 và f C Đ = 5
Mặt khác, ta có f(-4) = f(4) = 3
Vậy 
d) f(x) = | x 2 − 3x + 2| trên đoạn [-10; 10]
Khảo sát sự biến thiên và vẽ đồ thị của hàm số g(x) = x 2 – 3x + 2.
Ta có:
g′(x) = 2x − 3; g′(x) = 0 ⇔ x = 3/2
Bảng biến thiên:
Vì
nên ta có đồ thị f(x) như sau:
Từ đồ thị suy ra: min f(x) = f(1) = f(2) = 0; max = f(x) = f(−10) = 132
e) 
f′(x) < 0 nên và f’(x) > 0 trên (π/2; 5π/6] nên hàm số đạt cực tiểu tại x = π/2 và f C T = f(π/2) = 1
Mặt khác, f(π/3) = 2√3, f(5π/6) = 2
Vậy min f(x) = 1; max f(x) = 2
g) f(x) = 2sinx + sin2x trên đoạn [0; 3π/2]
f′(x) = 2cosx + 2cos2x = 4cos(x/2).cos3(x/2)
f′(x) = 0
⇔ 
Ta có: f(0) = 0,
Từ đó ta có: min f(x) = −2 ; max f(x) = 3√3/2
Đúng 0
Bình luận (0)