Một chuyển động thẳng xác định bởi phương trình s = t 3 – 3 t 2 + 5 t + 2 , trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t = 3 là:
A. 24 m / s 2
B. 17 m / s 2
C. 14 m / s 2
D. 12 m / s 2
Một chuyển động thẳng xác định bởi phương trình s = t 3 - 3 t 2 + 5 t + 2 , trong đó t tính bằng giây và S tính bằng mét. Gia tốc của chuyển động khi t = 3 là:
A. 24 m / s 2
B. 17 m / s 2
C. 14 m / s 2
D. 12 m / s 2
Đáp án D
Ta có gia tốc tức thời của chuyển động tại thời điểm t bằng đạo hàm cấp hai của phương trình chuyển động tại thời điểm t.
s ' = t 3 - 3 t 2 + 5 t + 2 ' = 3 t 2 - 6 t + 5
s ' ' = 6 t - 6 ⇒ s ' ' 3 = 12
Một chuyển động thẳng xác định bởi phương trình s = t 3 - 3 t 2 + 5 t + 2 , trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t=3 là:
A. 24 m / s 2
B. 17 m / s 2
C. 14 m / s 2
D. 12 m / s 2
Một chuyển động thẳng xác định bởi phương trình s = t 3 – 3 t 2 + 5 t + 2 , trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t= 3 là:
A. 24 m / s 2
B. 17 m / s 2
C. 14 m / s 2
D. 12 m / s 2
Đáp án D
- Ta có gia tốc tức thời của chuyển động tại thời điểm t bằng đạo hàm cấp hai của phương trình chuyển động tại thời điểm t.
- Ta có:
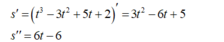
- Suy ra, phương trình gia tốc của chuyển động là:
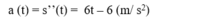
- Do đó, gia tốc của chuyển động khi t = 3 là: a(3) = 12 m / s 2
Một chuyển động thẳng xác định bởi phương trình \(s\left( t \right) = 4{t^3} + 6t + 2\), trong đó \(s\) tính bằng mét và \(t\) là thời gian tính bằng giây. Tính vận tốc tức thời của chuyển động tại \(t = 2\).
Vận tốc tức thời của chuyển động tại \(t = 2\) là:
\(\begin{array}{l}v\left( 2 \right) = s'\left( 2 \right) = \mathop {\lim }\limits_{t \to 2} \frac{{s\left( t \right) - s\left( 2 \right)}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{\left( {4{t^3} + 6t + 2} \right) - \left( {{{4.2}^3} + 6.2 + 2} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t + 2 - 46}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{4{t^3} + 6t - 44}}{{t - 2}} = \mathop {\lim }\limits_{t \to 2} \frac{{2\left( {t - 2} \right)\left( {2{t^2} + 4t + 11} \right)}}{{t - 2}}\\ = \mathop {\lim }\limits_{t \to 2} 2\left( {2{t^2} + 4t + 11} \right) = 2\left( {{{2.2}^2} + 4.2 + 11} \right) = 54\end{array}\)
Vậy vận tốc tức thời của chuyển động lúc \(t = 2\) là: \(v\left( 2 \right) = 54\left( {m/s} \right)\)
Một chất điểm chuyển động thẳng đều được xác định bởi phương trình : s = 54t + 2, trong đó t tính bằng giây và s tính bằng mét. Gia tốc của chuyển động khi t = 3 là:
A. 24 m/s2.
B. 17 m/s2.
C. 14 m/s2.
D. Tất cả sai
Chọn D.
Gia tốc chuyển động tại t = 3s là s”(3)
Ta có: s’(t) = 54 và s’’(t) = 0
Vậy vật chuyển động với gia tốc là 0 nên tại t = 3 thì a = 0.
Một chất điểm chuyển động thẳng được xác định bởi phương trình : s(t) : t3 + 5t2 + 5, trong đó t tính bằng giây và s tính bằng mét. Tính gia tốc của chuyển động khi t = 2.
A : 10
B : 12
C : 14
D : 16
Chọn B.
Ta có s’(t) = 3t2 + 10t ; s”(t) = 6t.
Do đó gia tốc chuyển động có phương trình a(t) = 6t.
Gia tốc của chuyển động tại t = 2 là : a(2) = 6.2 = 12
Một vật chuyển động thẳng xác định bởi phương trình S = t 3 - 3 t 2 + 5 t + 1 , trong đó t tính bằng giây (s), S tính bằng mét. Vận tốc chuyển động của vật đó khi t=3 là:
A. 24(m/s)
B. 17(m/s)
C. 14(m/s)
D. 12(m/s)
Một vật chuyển động thẳng xác định bởi phương trình S = t 3 − 3 t 2 + 5 t + 1 trong đó t tính bằng giây và S tính bằng mét. Vận tốc chuyển động của vật đó khi t=3 là
A. 12 (m/s)
B. 14 (m/s)
C. 17 (m/s)
D. 24 (m/s)
Đáp án B
Vận tốc của vật xác định bởi phương trình v = s ' = 3 t 2 − 6 t + 5 ⇒ v 3 = 14 m / s
Một chất điểm chuyển động thẳng xác định bởi phương trình s(t) = 2t3 – 2t2 + 6 trong đó t là giây ; s là mét. Tính vận tốc của chuyển động khi t = 1
A : 1
B : 2
C : 3
D : Đáp án khác
Chọn B.
Ta có: s’(t) = 6t2 – 4t
Nên phương trình vận tốc của chuyển động là: v(t) = 6t2 – 4t (m/s)
Vận tốc của vật khi t = 1 là: v(1) = 6.1 - 4.1 = 2(m/s)