Trong không gian cho đường thẳng a ⊂ ( α ) , b ⊂ ( β ) , ( α ) / / ( β . Kết quả nào sau đây là đúng?
A. a//b
B. a, b chéo nhau
C. a, b cắt nhau
D. a, b không có điểm chung
Trong không gian cho đường thẳng a ⊂ α , b ⊂ β , α / / β . Kết quả nào sau đây là đúng?
A. a//b
B. a,b chéo nhau
C. a,b cắt nhau
D. a,b không có điểm chung
Trong không gian cho đường thẳng a ⊂ α , b ⊂ β / / β . Kết quả nào sau đây là đúng?
A. a//b
B. a,b chéo nhau
C. a,b cắt nhau
D. a,b không có điểm chung
Trong không gian với hệ tọa độ Oxyz cho hai điểm A a ; 0 ; - 2 và B 2 ; b ; 0 . Gọi α là mặt phẳng chứa A và trục Oy; β là mặt phẳng chứa B và trục Oz. Biết rằng α và β cắt nhau theo giao tuyến là đường thẳng ∆ có vectơ chỉ phương u → = 2 ; 1 ; 2 . Tính độ dài đoạn thẳng AB
A. A B = 5
B. A B = 2 2
C. A B = 21
D. A B = 2 6

Mặt phẳng
α
chứa A và trục Oy nên có một VTPT là ![]()
Đường thẳng
∆
là giao tuyến của
α
và
β
nên có VTCP ![]()
Theo giả thiết, ta có
u
∆
→
cùng phương với ![]()
Suy ra 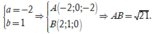
Chọn C.
Trong không gian Oxyz cho mặt phẳng (α) có phương trình 4x + y + 2z + 1 =0 và mặt phẳng ( β) có phương trình 2x – 2y + z + 3 = 0
Viết phương trình tham số của đường thẳng d là giao của (α) và ( β)
Cho hai mặt phẳng song song α và β. Đường thẳng d nằm trong α (h.2.47). Hỏi d và β có điểm chung không?
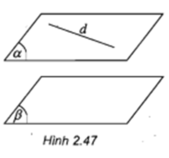
Hai mặt phẳng song song α và β ⇒ α và β không có điểm chung
Đường thẳng d nằm trong α ⇒ Đường thẳng d không thể cắt mặt phẳng β. Vì nếu d cắt mặt phẳng β tức là d và β có điểm chung
=> hai mặt phẳng α và β có điểm chung (mâu thuẫn với giả thiết)
Vậy d và β không có điểm chung
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến m. Trên đường thẳng d cắt (α) ở A và cắt (β) ở B ta lấy hai diểm cố định S 1 , S 2 không thuộc (α), (β). Gọi M là một điểm di động trên (β). Giả sử các đường thẳng M S 1 , M S 2 cắt (α) lần lượt tại M 1 và M 2 .
a) Chứng minh rằng M 1 M 2 luôn luôn đi qua một điểm cố định.
b) Giả sử đường thẳng M 1 M 2 cắt giao tuyến m tại K. Chứng minh rằng ba điểm K, B, M thẳng hàng.
c) Gọi b là một đường thẳng thuộc mặt phẳng (β) nhưng không đi qua điểm B và cắt m tại I. Chứng minh rằng khi M di động trên b thì các điểm M 1 và M 2 di động trên hai đường thẳng cố định thuộc mặt phẳng (α).
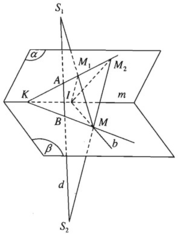
a) Mặt phẳng (M, d) cắt (α) theo giao tuyến M 1 M 2 . Điểm A cũng thuộc giao tuyến đó. Vậy đường thẳng M 1 M 2 luôn luôn đi qua điểm A cố định.
b) Mặt phẳng (M, d) cắt (β) theo giao tuyến BM. Điểm K thuộc giao tuyến đó nên ba điểm K, B, M thẳng hàng.
c) Giả sử b cắt m tại I thì mặt phẳng ( S 1 , b ) luôn luôn cắt (α) theo giao tuyến I M 1 . Do đó điểm M 1 di động trên giao tuyến của I M 1 cố định. Còn khi M di động trên b thì mặt phẳng ( S 2 , b ) cắt (α) theo giao tuyến I M 2 . Do đó điểm M 2 chạy trên giao tuyến I M 2 cố định.
Cho hai mặt phẳng (α) và (β) cắt nhau theo giao tuyến d. Trong (α) lấy hai điểm A và B sao cho AB cắt d tại I. O là một điểm nằm ngoài (α) và (β) sao cho OA và OB lần lượt cắt (β) tại A’ và B’.
a) Chứng minh ba điểm I, A’, B’ thẳng hàng.
b) Trong (α) lấy điểm C sao cho A, B, C không thẳng hàng. Giả sử OC cắt (β) tại C’, BC cắt B’C’ tại J, CA cắt C’A’ tại K. Chứng minh I, J, K thẳng hàng.
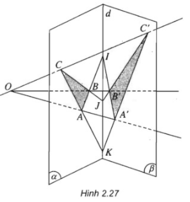
a) I, A’, B’ là ba điểm chung của hai mặt phẳng (OAB) và (β) nên chúng thẳng hàng.
b) I, J, K là ba điểm chung của hai mặt phẳng (ABC) và (A’B’C’) nên chúng thẳng hàng.
Cho hai mặt phẳng (α) và (β) song song với nhau. Đường thẳng a cắt (α) và (β) lần lượt tại A và C. Đường thẳng b song song với a cắt (α) và (β) lần lượt tại B và D.
Hình 2.72 minh họa nội dung trên đúng hay sai?
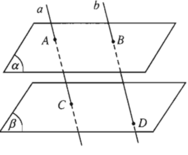
Sai vì
Ta có định lí 3 trang 67: cho hai mặt phẳng song song. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến song song
Theo đề bài ta có: (α) // (β)
a//b nên A,B,C,D thuộc mặt phẳng
AB là giao tuyến của (α) và (ABDC)
CD là giao tuyến của (β) và (ABDC)
⇒ AB // CD (theo định lí)
Hình 2.72 không biểu diễn được AB // CD
Trong không gian với hệ tọa đọ Oxyz, gọi ( α ) là mặt phẳng chứa đường thẳng ∆ có phương trình x - 2 1 = y - 1 1 = z 1 và vuông góc với mặt phẳng β : x+y-2z-1=0. Giao tuyến của ( α ) và β đi qua điểm nào trong các điểm sau:
A. A(2;1;1)
B. C(1;2;1)
C. D(2;1;0)
D. B(0;1;0)