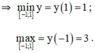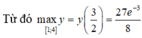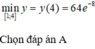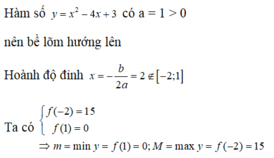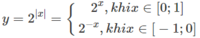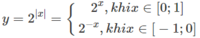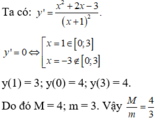Giá trị lớn nhất và nhỏ nhất của hàm số y = 4x - 2x+1 trên đoạn [- 1;1]
A. m i n - 1 ; 1 y = - 3 4 ; m a x - 1 ; 1 y = 2
B. m i n - 1 ; 1 y = - 3 4 ; m a x - 1 ; 1 y = 0
C. m i n - 1 ; 1 y = - 1 ; m a x - 1 ; 1 y = 1
D. m i n - 1 ; 1 y = - 1 ; m a x - 1 ; 1 y = 0


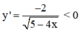 với ∀ x ∈ (-∞; 5/4)
với ∀ x ∈ (-∞; 5/4)