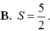Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
y
-
5
2
z
-
2
1
,
d
:
x
-...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
:
x
-
2
1
=
y
-
5
2
=
z
-
2
1
,
d
'
:
x
-
2
1
=
y
-
1
-
2
=
z
-
2
1
và hai điểm
A
a
;
0
;
0
,
A
'
0
;
0
;
b
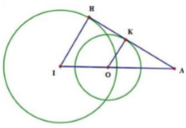
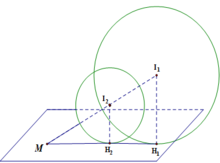
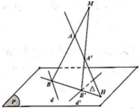
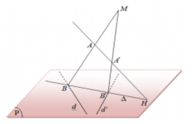
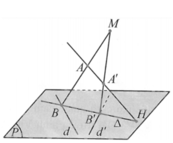
. Gọi (P) là mặt phẳng chứa d và d '; H là giao điểm của đường thẳng AA' và mặt phẳng (P). Một đường thẳng
∆
thay đổi trên (P) nhưng luôn đi qua H đồng thời
∆
cắt d và d ' lần lượt là B, B '. Hai đường thẳng AB, A'B' cắt nhau tại điểm M. Biết điểm M luôn thuộc một đường thẳng cố định có vectơ chỉ phương
u
→
=
15
;
-
10
;
-
1
(tham khảo hình vẽ). Tính T= a+b
A. T = 8
B. T = 9
C. T = - 9
D. T = 6