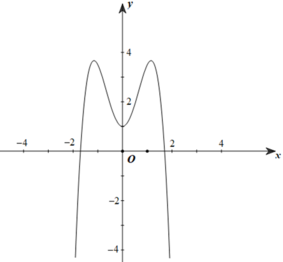
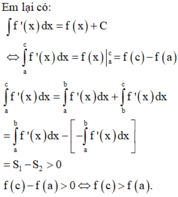Cho hàm số y = a x 4 + b x 2 + c có đồ thị như hình vẽ .
Mệnh đề nào dưới đây đúng?
A. a>0, b<0, c>0
B. a<0, b>0, c<0
C. a>0, b<0, c<0
D. a<0, b<0, c<0.
Cho hàm số y = f(x) liên tục trên [a;b] có đồ thị hàm số y = f'(x) như hình vẽ sau: Mệnh đề nào dưới đây đúng?
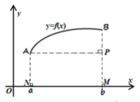
A. ∫ a b f ' ( x ) d x là diện tích hình thang cong ABMN
B. ∫ a b f ' ( x ) d x là độ dài đoạn BP.
C. ∫ a b f ' ( x ) d x là độ dài NM.
D. ∫ a b f ' ( x ) d x là độ dài đoạn cong AB
Cho hàm số y =f(x) liên tục trên [a;b] có đồ thị hàm số y = f ' (x) như hình vẽ sau: Mệnh đề nào dưới đây đúng?
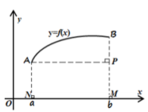
A. ∫ a b f ' x d x là diện tích hình thang cong ABMN
B. ∫ a b f ' x d x là độ dài đoạn BP
C. ∫ a b f ' x d x là độ dài NM
D. ∫ a b f ' x d x là độ dài đoạn cong AB
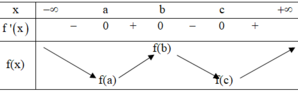
Cho hàm số y = f(x) có đồ thị y = f ' (x) cắt trục Ox tại ba điểm có hoành độ a<b<c như hình vẽ
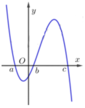
Xét 4 mệnh đề sau
1 : f c > f a > f b 2 : f c > f b > f a 3 : f a > f b > f c 4 : f a > f b
Trong các mệnh đề trên có bao nhiêu mệnh đề đúng
A. 4
B. 1
C. 2
D. 3
Đáp án C
Trên khoảng ( a, b )ta có: f ' (x)< 0 nên hàm số nghịch biến trên khoảng (a, b)
Ta có f (a) > f (b)
Tương tự trên khoảng ( b,c ) có f ' ( x ) > 0 nên hàm số đồng biến trên ( b,c )suy ra f (c) > f (b)
(Đến đây rõ ràng ra suy ra được 4 đúng và 1 trong 2 ý (1) và (2) có 1 ý đúng ta sẽ suy ra đáp án cần chọn là C)
Chặt chẽ hơn: Dựa vào đồ thị ta thấy
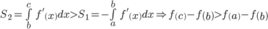 Do đó f (c) > f (a) > f (b)
Do đó f (c) > f (a) > f (b)
Cho hàm số f(x) = ax4 + bx2 + c (a ≠ 0) có đồ thị hàm số như hình vẽ:
Tìm mệnh đề đúng trong các mệnh đề sau:
A. a > 0; b < 0; c > 0
B. a < 0; b > 0; c < 0
C. a < 0; b < 0; c > 0
D. a < 0; b > 0; c > 0
Cho hàm số y = f(x), biết tại các điểm A, B, C đồ thị của hàm số y = f(x) có tiếp tuyến được thể hiện như hình vẽ bên. Mệnh đề nào dưới đây đúng?
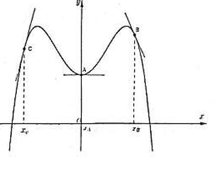
A . f ' ( x C ) < f ' ( x A ) < f ' ( x B ) .
B . f ' ( x A ) < f ' ( x B ) < f ' ( x C ) .
C . f ' ( x A ) < f ' ( x C ) < f ' ( x B ) .
D . f ' ( x B ) < f ' ( x A ) < f ' ( x C ) .
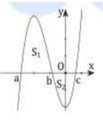
Cho hàm số y=f(x) có đồ thị y=f '(x) cắt trục Ox tại ba điểm có hoành độ a<b<c như hình vẽ.
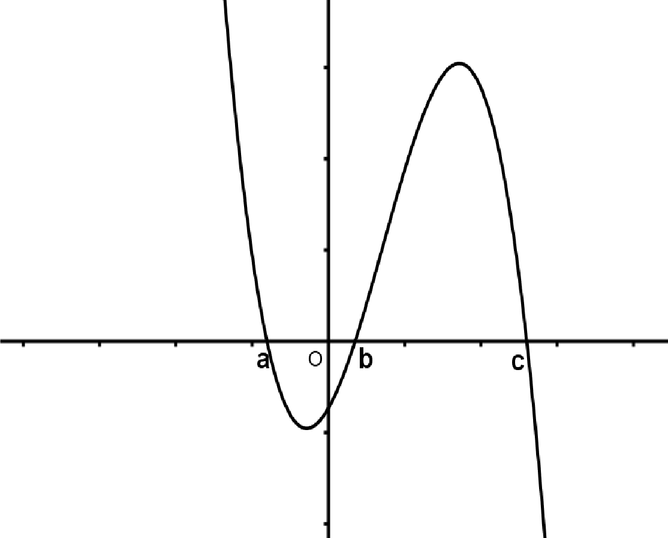
Mệnh đề nào dưới đây là đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Chọn A
Đồ thị của hàm số ![]() liên tục trên các đoạn
liên tục trên các đoạn ![]() và
và ![]() , lại có
, lại có ![]() là một nguyên hàm của
là một nguyên hàm của ![]() .
.
Do đó diện tích của hình phẳng giới hạn bởi các đường:
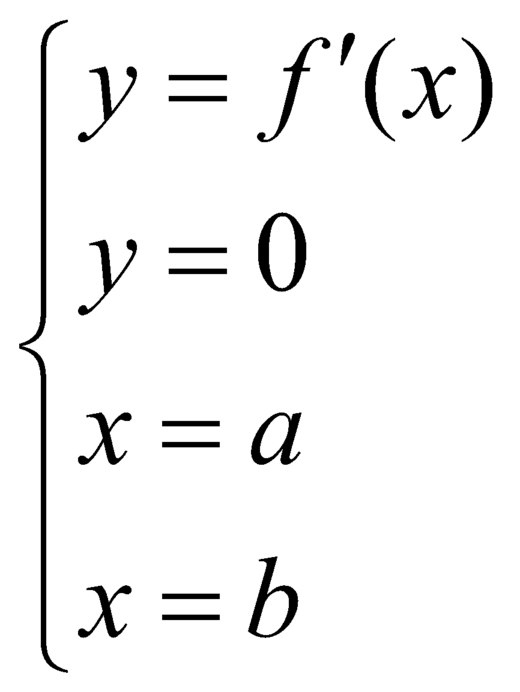 là:
là:
![]() .
.
Vì ![]()
![]()
Tương tự: diện tích của hình phẳng
giới hạn bởi các đường: 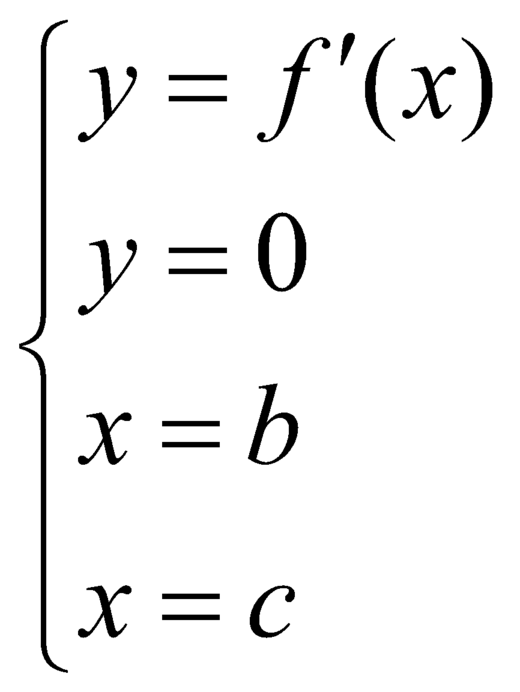 là:
là:
![]() .
.
![]()
![]() .
.
Mặt khác, dựa vào hình vẽ ta có: ![]()
![]() .
.
Từ (1), (2) và (3) ta chọn đáp án A.
( có thể so sánh ![]() với
với ![]() dựa vào dấu của
dựa vào dấu của ![]() trên đoạn
trên đoạn ![]() và so sánh
và so sánh ![]() với
với ![]() dựa vào dấu của
dựa vào dấu của ![]() trên đoạn
trên đoạn ![]() )
)
Cho hàm số y = f(x) có đồ thị y = f’(x) cắt trục Ox tại 3 điểm có hoành độ a<b<c như hình vẽ. Mệnh đề nào dưới đây là đúng
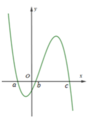
A. f(a)>f(b)>f(c)
B. f(c)>f(b)>f(a)
C. f(c)>f(a)>f(b)
D. f(b)>f(a)>f(c)
Đáp án C
Phương pháp:
+) ![]() đồng biến trên (a;b)
đồng biến trên (a;b)
+) ![]() nghịch biến trên (a;b)
nghịch biến trên (a;b)
Cách giải:
Quan sát đồ thị của hàm số y = f’(x), ta thấy:
+) ![]() đồng biến trên (a;b) => f(a) > f(b)
đồng biến trên (a;b) => f(a) > f(b)
+) ![]() nghịch biến trên (b;c) => f(b)<f(c)
nghịch biến trên (b;c) => f(b)<f(c)
Như vậy, f(a)>f(b), f(c)>f(b)
Đối chiếu với 4 phương án, ta thấy chỉ có phương án C thỏa mãn
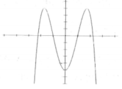
Cho hàm số f x = 3 2 x - 2 . 3 x có đồ thị như hình vẽ sau
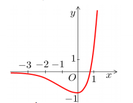
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại điểm có hoành độ là x = log 3 2
(2) Bất phương trình f x ≥ - 1 có nghiệm duy nhất.
(3) Bất phương trình f x ≥ 0 có tập nghiệm là - ∞ ; log 3 2
(4) Đường thẳng y = 0 cắt đồ thị hàm số (C) tại 2 điểm phân biệt.
A. 2
B. 4
C. 1
D. 3
Đáp án C
Dựa vào đáp án, ta thấy rằng
(1) Đường thẳng f x = 0 ⇔ 3 2 x - 2 . 3 x = 0 ⇔ 3 x = 2 ⇔ x = log 3 2 ⇒ 1 đúng.
(2) Bất phương trình f x ≥ - 1 ⇔ 3 2 x - 2 . 3 x + 1 ≥ 0 ⇔ 3 x - 1 2 ≥ 0 , ∀ x ∈ ℝ . Nên f x ≥ - 1 có vô số nghiệm ⇒ 2 sai.
(3) Bất phương trình f x ≥ 0 ⇔ 3 x 2 - 2 . 3 x ≥ 0 ⇔ 3 x ≥ 2 ⇔ x ≥ log 3 2 ⇒ 3 sai.
(4) Đường thẳng f(x) = 0 chỉ có 1 nghiệm duy nhất ⇒ 4 sai
Cho hàm số f x = 3 2 x − 2.3 x có đồ thị như hình vẽ sau
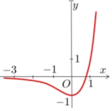
Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Đường thẳng y=0 cắt đồ thị hàm số (C) tại điểm có hoành độ là
x
=
log
3
2
(2) Bất phương trình
f
x
≥
−
1
có nghiệm duy nhất.
(3) Bất phương trình
f
x
≥
0
có tập nghiệm là
−
∞
;
log
3
2
(4) Đường thẳng y=0 cát đồ thị hàm số (C) tại 2 điểm phân biệt
A. 2.
B. 4.
C. 1.
D. 3.
Cho hàm số y = f(x) có đồ thị y = f '(x) cắt trục hoành tại ba điểm phân biệt có hoành độ a < b < c như hình vẽ. Mệnh đề nào dưới đây là đúng?
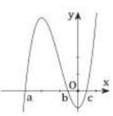
A. f b > f c > f a .
B. f a > f b > f c .
C. f c > f b > f a .
D. f b > f a > f c .
Đáp án A
Dựa vào đồ thị của hàm số y = f '(x), em suy ra được bảng biến thiên như sau: