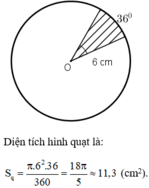
Tính diện tích một hình quạt tròn có bán kính 6cm, số đo cung là 36 °
PB
Những câu hỏi liên quan
Tính diện tích một hình quạt tròn có bán kính 6cm, số đo cung là 36o.
Tính diện tích một hình quạt tròn có bán kính 6 cm, số đo cung là 36o.
Theo công thức S = ta có S=
≈ 3,6π (cm2)
Đúng 0
Bình luận (0)
Tính diện tích một hình quạt tròn có bán kính 6cm, số đo cung là 36o Đáp án và hướng dẫn giải bài 79: Diện tích hình quạt ∠OAB có OA = 6cm, cung AOB =36o Theo công thức S = ΠR2no/360o Ta có S= Π62.36/360 ≈ 3,6π = 11,30(cm2)
Đúng 0
Bình luận (0)
Theo công thức S = ta có S=
≈ 3,6π (cm2)
Đúng 0
Bình luận (0)
Bài 1;Chân một đồng cát đổ trên một nền phẳng nằm ngang là một hình tròn có chu vi 12m. Hỏi chân đống cát đó chiếm một diện tích là bao nhiêu mét vuông?
Bài 2:Tính diện tích một hình quạt tròn có bán kính 6cm, số đo cung là 36o.
con me may cho de
Chắc là học sinh Thanh Bình của quận Tân Bình rồi :(
Tính diện tích hình quạt có bán kính 6cm, số đo cung là
36
0
A.
2
3
π
c
m
2
B.
18
5
π
c
m
2
C.
13
5
π
c
m
2
D. ...
Đọc tiếp
Tính diện tích hình quạt có bán kính 6cm, số đo cung là 36 0
A. 2 3 π c m 2
B. 18 5 π c m 2
C. 13 5 π c m 2
D. 4 3 π c m 2
Đáp án là B
Diện tích hình quạt tròn bán kính R, cung n 0 là
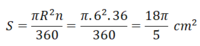
Đúng 0
Bình luận (0)
Tính diện tích hình tròn có bán kính 6 cm số đo cung là 36°
Ta có công thức S =\(\frac{\pi R^2n^o}{360^o}\)
=> S = \(\frac{\pi6^2.36}{360}\)= \(3,6\pi\left(cm^2\right)\)
k cho mk nha
Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:
Hình tròn bán kính R (ứng với cung 360o) có diện tích là … .
Vậy hình quạt tròn bán kính R, cung 1o có diện tích là … .
Hình quạt tròn bán kính R, cung no có diện tích S = … .
Hình tròn bán kính R (ứng với cung 360o) có diện tích là πR2
Vậy hình quạt tròn bán kính R, cung 1o có diện tích là (πR2)/360
Hình quạt tròn bán kính R, cung no có diện tích S = (πR2n)/360
Đúng 0
Bình luận (0)
Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:Hình tròn bán kính R (ứng với cung
360
°
) có diện tích là … .Vậy hình quạt tròn bán kính R, cung
1
°
có diện tích là … .Hình quạt tròn bán kính R, cung
n
°
có diện tích S … .
Đọc tiếp
Hãy điền biểu thức thích hợp vào các chỗ trống (…) trong dãy lập luận sau:
Hình tròn bán kính R (ứng với cung 360 ° ) có diện tích là … .
Vậy hình quạt tròn bán kính R, cung 1 ° có diện tích là … .
Hình quạt tròn bán kính R, cung n ° có diện tích S = … .
Hình tròn bán kính R (ứng với cung 360 ° ) có diện tích là π R 2
Vậy hình quạt tròn bán kính R, cung 1 ° có diện tích là π R 2 / 360
Hình quạt tròn bán kính R, cung n ° có diện tích S = π R 2 n / 360
Đúng 0
Bình luận (0)
Bài3: tính diện tích một hình quạt có bán kính 6 m số đo cũng là 36°
Theo công thức S = \(\frac{\pi R^2n^o}{360^0}\) ta có S=\(\frac{\pi6^2.36}{360}\) \(\approx\) 3,6\(\pi\) ( cm\(^2\))
@hc tốt !!
#Ji_en *quẹc*
Một hình quạt tròn bán kính R=4/√π, cung 90°. Tính diện tích hình quạt đó
S quạt = \(\dfrac{\pi.R^{2^{ }}.n^o}{360}\)=\(\dfrac{\pi.\left(\dfrac{4}{\sqrt{\pi}}\right)^2.90}{360}\)=4(đ/v diện tích)
Đúng 1
Bình luận (0)