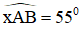Dựng một cung chứa góc 55 0 trên đoạn thẳng AB = 3cm
PB
Những câu hỏi liên quan
Dựng một cung chứa góc 55 ° trên đoạn thẳng AB = 3cm.
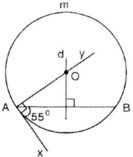
Cách dựng:
+ Dựng đoạn thẳng AB = 3cm.
+ Dựng góc 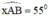
+ Dựng tia Ay vuông góc với tia Ax.
+ Dựng đường trung trực d của đoạn thẳng AB.
+ d cắt Ay tại O.
+ Dựng đường tròn tâm O, bán kính OA.
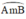 là cung chứa góc
55
º
cần dựng.
là cung chứa góc
55
º
cần dựng.
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒ 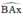 là góc tạo bởi tiếp tuyến Ax và dây AB
là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M ∈ 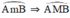 là góc nội tiếp chắn cung nhỏ
là góc nội tiếp chắn cung nhỏ 
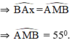
⇒ 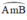 là cung chứa góc
55
º
dựng trên đoạn AB = 3cm.
là cung chứa góc
55
º
dựng trên đoạn AB = 3cm.
Kết luận: Bài toán có một nghiệm hình.
Đúng 0
Bình luận (0)
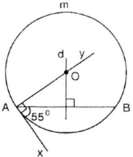
(Bài 46 SGK toán 9 tr.86) Dựng một cung chứa góc 55o trên đoạn thẳng AB = 3cm.
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc = 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
Dựng đoạn thẩng AB bằng 3cm dựng góc xAB =55* dựng tia AY vuông góc vs tia Ax dựng đg trung trực d của đoạn thẳng AB/ d cắt Ay tại O . Dựng đg tròn tâm O bán kính OA cung AmB là góc 55 độ cần dựng
Cách dựng:
+ Dựng đoạn thẳng AB = 3cm.
+ Dựng góc
+ D
ựng tia Ay vuông góc với tia Ax.
+ Dựng đường trung trực d của đoạn thẳng AB.
+ d cắt Ay tại O.
+ Dựng đường tròn tâm O, bán kính OA.
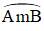
Xem thêm câu trả lời
Dựng một cung chứa góc 55o trên đoạn thẳng AB = 3cm.
Cách dựng:
+ Dựng đoạn thẳng AB = 3cm.
+ Dựng góc 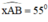
+ Dựng tia Ay vuông góc với tia Ax.
+ Dựng đường trung trực d của đoạn thẳng AB.
+ d cắt Ay tại O.
+ Dựng đường tròn tâm O, bán kính OA.
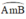 là cung chứa góc 55º cần dựng.
là cung chứa góc 55º cần dựng.
Chứng minh:
+ O thuộc đường trung trực của AB
⇒ OA = OB
QUẢNG CÁO⇒ B thuộc đường tròn (O; OA).
Ax ⊥ AO ⇒ Ax là tiếp tuyến của (O; OA).
⇒ 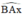 là góc tạo bởi tiếp tuyến Ax và dây AB
là góc tạo bởi tiếp tuyến Ax và dây AB
Lấy M ∈ 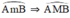 là góc nội tiếp chắn cung nhỏ
là góc nội tiếp chắn cung nhỏ 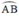
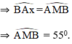
⇒  là cung chứa góc 55º dựng trên đoạn AB = 3cm.
là cung chứa góc 55º dựng trên đoạn AB = 3cm.
Kết luận: Bài toán có một nghiệm hình.
Đúng 0
Bình luận (0)
Dựng cung chứa góc \(42^0\) trên đoạn thẳng AB = 3cm
Dựng cung chứa góc 42 ° trên đoạn thẳng AB = 3cm
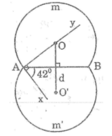
- Dựng đoạn thẳng AB = 3cm
- Vẽ tia Ax sao cho góc (BAx) = 42 °
- Dựng đường thẳng d là trung trực của đoạn AB
- Dựng tia Ay sao cho Ay ⊥ Ax (tia Ay cắt đường trung trực d của AB tại O)
- Dựng cung tròn AmB tâm O bán kính OA
- Dựng điểm O’ đối xứng với O qua AB
- Dựng cung tròn (Am'B) tâm O’ bán kính O’A
Ta được hai cung chứa góc 42 ° trên đoạn thẳng AB = 3cm đối xứng nhau qua AB
Đúng 0
Bình luận (0)
Dựng một cung chứa góc 55o trên đoạn thẳng AB = 3 cm.
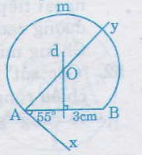
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc = 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: ![]() là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
Đúng 0
Bình luận (0)
Trình tự dựng như sau:
- Dựng đoạn thẳng AB = 3cm (dùng thước đo chia khoảng mm)
- Dựng góc \(\widehat{xAB}\)= 55o (dùng thước đo góc và thước thẳng)
- Dựng tia Ay vuông góc với Ax (dùng êke)
- Dựng đường trung trực d của đoạn thẳng AB (dùng thước có chi khoảng và êke). Gọi O là giao điểm của d và Ay.
- Dựng đường tròn tâm O, bán kính OA (dùng compa)
Ta có: ![]() là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
là cung chứa góc 55odựng trên đoạn thẳng AB = 3cm (một cung)
Đúng 0
Bình luận (0)
Dựng một cung chứa góc \(60^0\) trên đoạn thẳng AB cho trước ?

Lấy đối xứng qua đường thẳng AB, ta được cung chứa góc thứ hai thỏa mãn bài toán.
Chú ý : Cung nhỏ AB trong cách dựng trên là cung chứa góc \(120^0\)
Đúng 0
Bình luận (0)
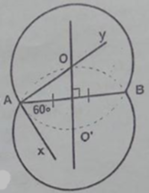
Dựng một cung chứa góc 60 ° trên đoạn thẳng AB cho trước.
Cách dựng: − Dựng đoạn thẳng AB.
− Dựng tia Ax sao cho góc BAx = 60 °
− Dựng đường thẳng d là trung trực của AB.
− Dựng tia Ay ⊥ Ax tại A.
− Tia Ay cắt đường thẳng d tại O.
− Dựng cung tròn tâm O bán kính OA.
− Dựng O' đối xứng với O qua AB.
− Dựng cung tròn tâm O’ bán kính O’A.
Ta có cung chứa góc 60° vẽ trên đoạn AB cho trước.
Đúng 0
Bình luận (0)
Quỹ tích các điểm M nhìn đoạn thẳng AB dưới một góc
120
°
là(A) một đường tròn đi qua hai điểm A, B.(B) một đường thẳng song song với AB.(C) một cung chứa góc
120
°
dựng trên hai điểm A, B.(D) hai cung chứa góc
120
°
(đối xứng nhau) dựng trên hai điểm A, B).
Đọc tiếp
Quỹ tích các điểm M nhìn đoạn thẳng AB dưới một góc 120 ° là
(A) một đường tròn đi qua hai điểm A, B.
(B) một đường thẳng song song với AB.
(C) một cung chứa góc 120 ° dựng trên hai điểm A, B.
(D) hai cung chứa góc 120 ° (đối xứng nhau) dựng trên hai điểm A, B).
Chọn (D) hai cung chứa góc 120° (đối xứng nhau) dựng trên hai điểm A, B).
Đúng 0
Bình luận (0)