Công thức tính độ lớn lực đàn hồi theo định luật Húc là:
A. F=ma
B. F = k △ l
C. F = μ N
D. F = G m 1 m 2 r 2
Theo định luật Húc về lực đàn hồi của lò xo thì độ lớn lực đàn hồi của lò xo được xác định bằng biểu thức nào sau đây ?
A. F đ h = 2 k △ l
B. F đ h = k △ l
C. F đ h = k ( △ l ) 2
D. F đ h = k 2 △ l
Đáp án B
Định luật Húc
Trong giới hạn đàn hồi, độ lớn của lực đàn hồi của lò xo tỉ lệ thuận với độ biến dạng của lò xo: 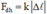
Trong đó:
+ k là độ cứng (hệ số đàn hồi) của lò xo, phụ thuộc vào hình dạng, kích thước và chất liệu của lò xo. Đơn vị của độ cứng là N/m.
+ 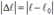 là độ biến dạng của lò
x
0
,
l
0
, ℓ lần lượt là chiều dài tự nhiên và chiều dài khi biến dạng của lò xo.
là độ biến dạng của lò
x
0
,
l
0
, ℓ lần lượt là chiều dài tự nhiên và chiều dài khi biến dạng của lò xo.
Từ định luật Húc về biến dạng cơ của vật rắn, hãy suy ra công thức của lực đàn hồi trong vật rắn.
Trong giới hạn đàn hồi, độ biến dạng tỉ đối của vật rắn hình trụ tỉ lệ với ứng suất gây ra nó: 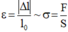
Có thể viết:  là hệ số tỉ lệ (E là suất đàn hồi đơn vị là Pa)
là hệ số tỉ lệ (E là suất đàn hồi đơn vị là Pa)
Suy ra: 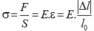
(E là suất đàn hồi, đơn vị là Pa ; S: Diện tích tiết diện của vật rắn đồng chất, hình trụ. lo: Chiều dài ban đầu của vật).
Chú ý: Với 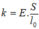 là hệ số đàn hồi hay độ cứng của thanh rắn, thì lực đàn hồi tính theo biểu thức:
là hệ số đàn hồi hay độ cứng của thanh rắn, thì lực đàn hồi tính theo biểu thức: 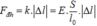
Đặt F → là hợp lực của tất cả các lực tác dụng vào vật có khối lượng m. Định luật II Niu tơn có công thức a → = F → m h a y F → = m a → . Tìm phát biểu sai dưới đây trong vận dụng định luật.
A. Áp dụng cho chuyển động rơi tự do ta có công thức trọng lượng P → = m g →
B. Vật chịu tác dụng của lực luôn chuyển động theo chiều của hợp lực F → .
C. Khối lượng m càng lớn thì vật càng khó thay đổi vận tốc.
D. Nếu vật là chất điểm thì điều kiện cân bằng của vật là F → = 0
Từ định luật Húc về biến dạng cơ của vật rắn, hãy suy ra công thức của lực đàn hồi trong vật rắn.
Hướng dẫn giải:
Trong giới hạn đàn hổi, độ biến dạng tỉ đối của thanh rắn tỉ lệ thuận với ứng suất của lực kéo thanh đó:
\(\dfrac{\Delta l}{l_0}=\alpha\sigma\)
với α là hệ số tỉ lệ phụ thuộc chấ liệu của thanh rắn.
Lực đàn hồi Fđh tỉ lệ với độ biến dạng ∆l = |l – l0| của thanh rắn:
\(F_{đh}=k\Delta l\) với \(k=E\dfrac{S}{l_0}\)
Trong đó:
\(E=\dfrac{1}{a}=\) suất đàn hồi đặc trưng cho tính đàn hồi của thanh rắn.
Đơn vị của E là paxcan (Pa).
k = độ cứng của thanh rắn phụ thuộc chất liệu và kích thước cuả thanh.
Đơn vị đo của k là N/m
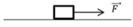
Một vật có khối lượng m = 5kg trượt trên mặt phẳng nằm ngang nhờ lực kéo F → như hình vẽ. Cho biết: độ lớn lực kéo F = 20N; g = 10m/ s 2
a) Tính gia tốc của vật, khi bỏ qua mọi ma sát ?
b) Tính gia tốc của vật, khi hệ số ma sát trượt giữa vật và mặt phẳng là μ = 0,2?
a) (2 điểm)
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật: (0,5 điểm)
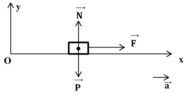
+ Viết phương trình định luật II Niu-tơn: 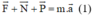 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (1) lên trục Ox ta được: F = m.a (0,5 điểm)
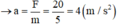 (0,5 điểm)
(0,5 điểm)
b) (2 điểm)
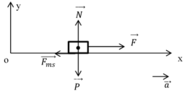
+ Vẽ hình, biểu diễn tất cả mọi lực tác dụng lên vật
+ Viết phương trình định luật II Niu-tơn
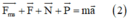 (0,5 điểm)
(0,5 điểm)
+ Chiếu pt (2) lên trục Oy: N – P = 0
→ N = P = m.g = 5.10 = 50N (0,5 điểm)
+ Độ lớn lực ma sát: F m s = μ.N = 0,2.50 = 10N (0,5 điểm)
+ Chiếu pt (2) lên trục Ox: F – F m s = ma
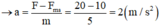 (0,5 điểm)
(0,5 điểm)
vật có khối lượng là 0,1 (kg) chuyển động theo phương nằm nghiêng 1 góc = 45 độ bởi lực F kéo theo mặt phẳng nghiêng , biết F=10 N (bỏ qua ma sát ) , g=10m/s^2
a) xác định các lực tác dụng lên vật
b) tính gia tốc,độ lớn các lực
b) Chọn hệ Oxy
Có : \(\overrightarrow{N}+\overrightarrow{P}+\overrightarrow{F}=m\overrightarrow{a}\leftrightarrow\overrightarrow{N}+\overrightarrow{P_1}+\overrightarrow{P_2}+\overrightarrow{F}=m\overrightarrow{a}\left(1\right)\)
Chiếu (1) lên Oy có: \(N-P_2=0\Leftrightarrow N-Pcos45^o=0\rightarrow N=mgcos45^o\)
Chiếu (1) lên Ox có :
\(Psin45^o-F_{ms}=Psin45^o-\mu mgcos45^o\)
=> a = \(g\left(sin45^o-0cos45^o\right)=10sin45^o=5\sqrt{2}\left(m/s^2\right)\)
b) P=mg = 0,1.1=1N
\(P_1=Psin45=mg.sin45=\frac{\sqrt{2}}{2}\left(N\right)\)
\(P_2=Pcos45=mgcos45=\frac{\sqrt{2}}{2}\left(N\right)\)
Khảo sát thực nghiệm một con lắc lò xo trên mặt phẳng ngang gồm vật nhỏ có khối lượng 100 g và lò xo có độ cứng k, dao động dưới tác dụng của ngoại lực F = F 0 cos 2 π f t , với F 0 không đổi và f thay đổi được. Với mỗi giá trị của f, dao động ổn định với biên độ A. Kết quả khảo sát ta được đường biểu diễn biên độ A của con lắc theo tần số f có đồ thị như hình vẽ.
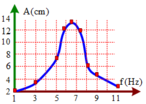
Ở tần số f = 5 H z , lực đàn hồi của lò xo có độ lớn cực đại xấp xỉ bằng
A. 9,8 N
B. 7,4 N
C. 15,2 N
D. 12,4N
Một sóng cơ có tần số f lan truyền trong môi trường đàn hồi với tốc độ là v, khi đó bước sóng được tính theo công thức
A. 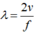
B. 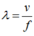
C. ![]()
D. ![]()
Đáp án B
Bước sóng được xác định bởi biểu thức 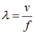
Một sóng cơ có tần số f lan truyền trong môi trường đàn hồi với tốc độ là v, khi đó bước sóng được tính theo công thức
A. λ = 2 v f
B. λ = v f
C. λ = v f
D. λ = 2 v f
Chọn B
Bước sóng λ của sóng cơ có tần số f, lan truyền trong môi trường với vận tốc v được xác định bằng biểu thức λ = v f