Cho hàm số y = f x có đồ thị là đường gấp khúc như hình vẽ bên. Tính ∫ 0 9 f x d x .

A. 18
B. 2
C. 0
D. 16
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho hàm số y = f ( x ) có đồ thị là đường gấp khúc như hình vẽ bên. Tính ∫ 0 9 f ( x ) d x .
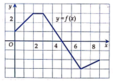
A. 18
B. 2
C. 0
D. 16
Cho hàm số y = f(x) có đồ thị trên đoạn [-1;4] là một đường gấp khúc như hình vẽ bên. Tính tích phân I = ∫ - 1 4 f x d x
A. I = 5 2
B. I = 3
C. I = 11 2
D. I = 5
Cho hàm số y=f(x) liên tục trên R và có đồ thị là đường cong như hình vẽ bên. Tìm điểm cực tiểu của đồ thị hàm số y=f(x).
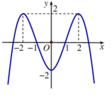
A. y=-2
B. x=0
C. M(0;-2)
D. N(2;2)
Đáp án C
Nhìn vào đồ thị thì điểm cực tiểu là điểm M(0;-2)
Cho hàm số y=f(x) có đồ thị (C) như hình vẽ bên và có đạo hàm f'(x) liên tục trên khoảng (-∞;+∞).Đường thẳng ở hình vẽ bên là tiếp tuyến của (C) tại điểm có hoành độ x=0. Gọi m là giá trị nhỏ nhất của hàm số y=f'(x). Mệnh đề nào dưới đây đúng ?
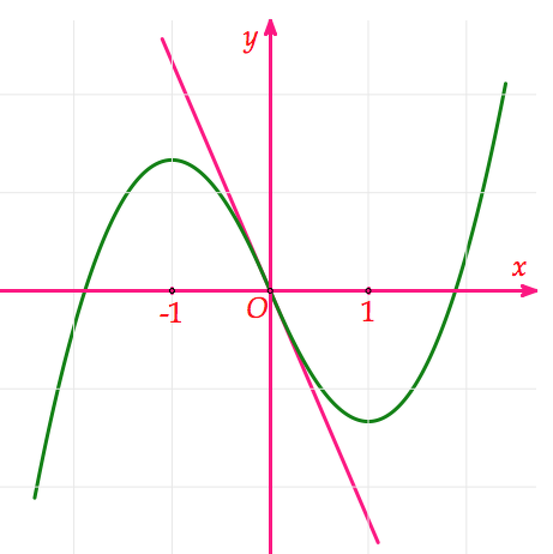
A. m < -2
B. -2 < m < 0.
C. 0 < m < 2
D. m > 2
Cho hàm số y=f(x) có đồ thị y=f’(x) như hình vẽ bên. Biết f(a)>0, hỏi đồ thị hàm số y=f(x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
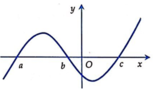
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
Cho hàm số y = f(x) có đồ thị y = f''(x) như hình vẽ bên. Biết f (a) > 0, hỏi đồ thị hàm số y = f (x) cắt trục hoành tại nhiều nhất bao nhiêu điểm?
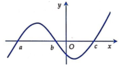
A. 1 điểm
B. 2 điểm
C. 3 điểm
D. 4 điểm
Đáp án B.
Từ đồ thị hàm số y = f ' ( x ) ta có bảng biến thiên:

Từ bảng biến thiên ta có f ( b ) > f ( a ) > 0
Quan sát đồ thị y = f ' ( x ) , dùng phương pháp tích phân để tính diện tích.
Ta có ∫ a b f ' ( x ) d x < ∫ a c 0 - f ' ( x ) d x ⇒ f ( c ) < f a
Nếu f c < 0 thì đồ thị hàm số y = f ( x ) cắt trục hoành tại 2 điểm phân biệt.
Nếu f c = 0 thì đồ thị hàm số y = f ( x ) tiếp xúc với trục hoành tại 1 điểm.
Nếu f c > 0 thì đồ thị hàm số y = f ( x ) không cắt trục hoành.
Vậy đồ thị hàm số y = f ( x ) cắt trục hoành tại nhiều nhất 2 điểm.
Cho hàm số y = f(x) liên tục trên R có đồ thị y = f'(x) như hình vẽ bên. Biết f 1 = 0 . Xác định số điểm cực trị của đồ thị hàm số y = |f(x)|.
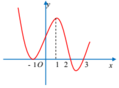
A. 5
B. 6
C. 4
D. 3
Đáp án D.
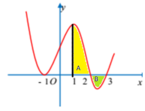
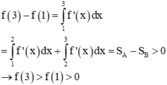
Đồ thị hàm số y = f(x) có dạng:
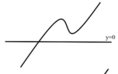
Đồ thị hàm số y = |f(x)| có dạng:
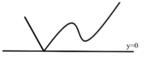
→ Hàm số y = |f(x)| có 3 điểm cực trị.
Cho hai hàm số y=f(x); y=g(x) có đạo hàm trên R và có đồ thị như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số y=f(x) Biết rằng hai hàm số y=f(-2x+1) và y = g a x + b a b ∈ ℝ ; a # 0 có cùng khoảng đồng biến. Giá trị của a + 2b bằng
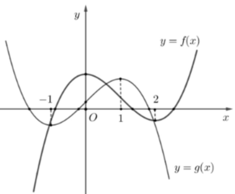
A. 3
B. 4
C. 2
D. 6
Với hàm số y=f(-2x+1) có
![]()
![]()
![]()
Với hàm số y=g(ax+b) có
y'=a.g'(ax+b)>0 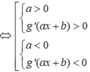
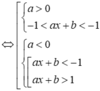
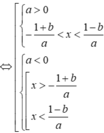
Vì hai hàm số đã cho có cùng khoảng đồng biến nên rơi vào trường hợp
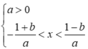 và
và 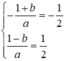
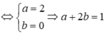
*Chú ý đồ thị đi lên hàm số đồng biến; đồ thị đi xuống hàm số nghịch biến.
Chọn đáp án C.
Cho hàm số y=f(x) có đạo hàm liên tục trên R. Hàm số y= f'(x) có đồ thị như hình vẽ bên dưới:
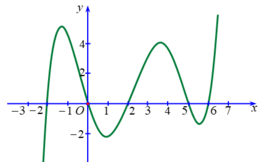
Số nghiệm thuộc đoạn [-2;6] của phương trình f(x) = f(0) là
A. 5
B. 2
C. 3
D. 4