Cho hình thoi ABCD. Giá trị của A B → + A D → . B A → + B C → là
A.1
B.0
C. A B 2 − B C 2
D. A B 2 + B C 2
Hình chữ nhật MNPQ có 4 đỉnh nằm trên 4 cạnh của hình thoi ABCD \(\left(M\in AB,N\in BC,P\in CD,Q\in DA\right)\). Các cạnh của hình chữ nhật song song với các đường chéo của hình thoi. Biết AB=7cm, \(\tan\widehat{BAC}=0,75\)
a, Tình diện tích hình thoi ABCD.
b, Xác định vị trí của điểm M trên cạnh AB sao cho diện tích hình chữ nhật MNP đạt giá trị lớn nhất và tính giá trị lớn nhất ấy.
cái hình thì mk gửi link trong ib nhé
a) Gọi O là giao điểm của AC và BD
\(\Delta OAB\) vuông tại O có \(OA^2+OB^2=AB^2=49\)
Lại có: \(\tan BAC=\tan OAB=\frac{OB}{OA}=\frac{3}{4}\)\(\Leftrightarrow\)\(\frac{OA^2}{16}=\frac{OB^2}{9}=\frac{OA^2+OB^2}{16+9}=\frac{49}{25}\)
\(\Rightarrow\)\(\hept{\begin{cases}\frac{OA}{4}=\frac{7}{5}\\\frac{OB}{3}=\frac{7}{5}\end{cases}}\Leftrightarrow\hept{\begin{cases}OA=\frac{28}{5}\left(cm\right)\\OB=\frac{21}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(\hept{\begin{cases}AC=2OA=\frac{56}{5}\left(cm\right)\\BD=2OB=\frac{42}{5}\left(cm\right)\end{cases}}\)
\(\Rightarrow\)\(S_{ABCD}=\frac{1}{2}AC.BD=\frac{1}{2}.\frac{56}{5}.\frac{42}{5}=\frac{1176}{25}=47,04\left(cm^2\right)\)
b) Gọi E, F lần lược là giao điểm của BD với MN và PQ
tam giác ABD có MQ // BD
\(\Rightarrow\)\(\frac{MQ}{BD}=\frac{MA}{AB}\) ( hệ quả định lí Talet )
tam giác OAD có QF // OA
\(\Rightarrow\)\(\frac{QF}{OA}=\frac{DQ}{AQ}=\frac{MB}{AB}\) ( hệ quả định lí Talet )
\(\Rightarrow\)\(\frac{MQ}{BD}+\frac{QF}{OA}=\frac{MA+MB}{AB}=1\)
\(\Rightarrow\)\(1\ge2\sqrt{\frac{MQ.QF}{BD.OA}}\)\(\Leftrightarrow\)\(MQ.QF\le\frac{1}{4}BD.OA\)
Tương tự, ta cũng có: \(NP.PF\le\frac{1}{4}BD.OC\)
\(\Rightarrow\)\(MQ.QF+NP.PF=S_{MEFQ}+S_{NEFP}=S_{MNPQ}\le\frac{1}{4}BD.AC=\frac{1}{2}S_{ABCD}=23,52\left(cm^2\right)\)
Dấu "=" xảy ra khi M, N, P, Q là trung điểm của AB, BC, CD, DA
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a và góc A B C ⏜ = 60 o . Các cạnh SA, SB, SC đều bằng a 3 2 . Gọi φ là góc của hai mặt phẳng (SAC) và (ABCD). Giá trị tan φ bằng bao nhiêu?
A. 2 5
B. 3 5
C. 5 3
D. 3
Đáp án A.
* Hướng dẫn giải:
Dễ thấy AB = BC và A B C ⏜ = 60 o nên tam giác ABC đều.
Gọi H là hình chiếu của A lên (ABCD).
Do SA = SB =SC nên H là tâm đường tròn ngoại tiếp tam giác ABC.
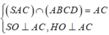
![]()
Mặt khác, H O = 1 3 B O = 1 3 . a 3 2 = a 3 6
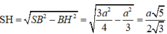
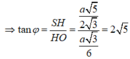
Hình chữ nhật mnpq có các đỉnh thuộc hình thoi abcd (m-ab, n-bc, p-dc) các. Cạnh của hcn song song với các đg chéo của hình thoi biết ab =7 tan bac =0.75 A diện tích abcd ;B vị trí của M trên ab đee hình chữ nhật mnpq có diện thích lớn nhát. Tính giá trị đó
Mn giúp mik .Thanks
Cho hàm số y = x 4 − 3 m x x − 2 m 2 + m 4 có đồ thị (C), biết đồ thị (C) có 3 điểm cực trị A, B, C và ABCD là hình thoi, trong đó D 0 ; − 3 thuộc trục tung. Khi đó các giá trị của tham số m thuộc khoảng nào dưới đây?
A. m ∈ − 1 ; 1 2 .
B. m ∈ 2 ; 3 .
C. m ∈ 9 5 ; 2 .
D. m ∈ 1 2 ; 9 5 .
Đáp án D.
Ta có: y ' = x 3 − 4 m x = 0 ⇔ x = 0 x 2 = m
Để hàm số có 3 điểm cực trị thì m > 0.
Khi đó tọa độ điểm cực trị là:
A 0 ; − 2 m 2 + m 4 ; B m ; m 4 − 3 m 2 ; C − m ; m 4 − 3 m 2
Do ABCD là hình thoi nên A B = B D ⇔ m + m 4 = m + m 4 − 3 m 2 + 3 2
⇔ m 2 = m 4 − 3 m 2 + 3 ⇔ m 4 − 4 m 2 + 3 = 0 ⇔ m = 1 m = 3 D o m > 0 .
Hai đường chéo của một hình thoi bằng 8cm và 10cm. Cạnh của hình thoi bằng giá trị nào trong các giá trị sau:
A. 6cm ; B. √41 cm ; c) √164cm ; d) 9cm
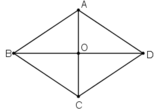
- Gọi ABCD là hình thoi, O là giao điểm hai đường chéo.
⇒ O là trung điểm của AC và BD.
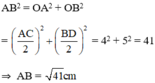
Vậy chọn đáp án là B.
Cho hình thoi ABCD, có cạnh a và Â= 60 độ, một đường thẳng qua C cắt tia đối của các tia BA, DA tại M,N
a) Cm: BM.DN không đổi giá trị
b) Gọi K là giao điểm của BN và DM. Tính góc BKD
Bài 1: Tìm giá trị của M để:
a, Tìm m : x2-(m-1).x+4 : (x-1)
b, Tìm a để đa thức f(x)=x4-5x2+a : g(x)=x2-3x+2
Bài 2: Cho hình thoi ABCD có cạnh AB=4 cm, góc A=60o . Tính Shình thoi đó?
(kẻ hình hộ mk ạ )
Ta có : \(\widehat{BAO}=\frac{1}{2}\widehat{BAD}=\frac{1}{2}60^o=30^o\)
Mà tam giác AOB vuông tại O, lại có \(\widehat{BAO}=30^o\)
\(\Rightarrow OB=\frac{1}{2}AB=\frac{1}{2}.4=2\left(cm\right)\)
Áp dụng định lý Pi- ta - go vào tam giác AOB có :
\(AO=\sqrt{AB^2-BO^2}=\sqrt{4^2-2^2}\)
\(=\sqrt{16-4}=\sqrt{12}\left(cm\right)\)
Có \(BO=2\Rightarrow BD=2BO=2.2=4\left(cm\right)\)
\(S_{htABCD}=\frac{1}{2}AC.BD=AO.BD=\sqrt{12}.4=8\sqrt{3}\left(cm^2\right)\)
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc BAD = 600 , SA=SB=SD= a 3 2 . Gọi α là góc giữa đường thẳng SD và mặt phẳng (SBC). Giá trị sin α bằng
A. 1 3
B. 2 3
C. 5 3
D. 2 2 3
Đáp án C
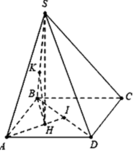
Gọi H là tâm đường tròn ngoại tiếp đều ∆ABD
Ta có 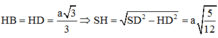
Lại có d(H;(SBC)) = HK và 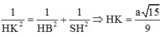
Khoảng cách từ D →(SBC) là 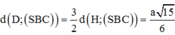
Vậy ∆ABD ![]()
Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm I, cạnh a, góc B A D ⏜ = 60 0 , SA=SB=SB= a 3 2 . Gọi α là góc giữa đường thẳng SD và mặt phẳng (SBC). Giá trị sin α bằng
A. 1 3
B. 2 3
C. 5 3
D. 2 2 3