Cho tam giác ABC có tâm đường tròn ngoại tiếp O. Tính H A → + H B ⇀ + H C ⇀
A. 2 H O →
B. H O →
C. A C →
D. Tất cả sai
Cho tam giác ABC có trực tâm H, trọng tâm G và tâm đường tròn ngoại tiếp O. Tính O A → + O B → + O C →
A. 2 O H →
B. O H →
C. A C →
D. Tất cả sai
Cho tam giác nhọn ABC,trực tâm H,nội tiếp đường tròn (o).Gọi H là trực đối xứng với A qua BC,Cm :a,Tứ giác ABHC nội tiếp ,b,Bán kính đường tròn ngoại tiếp tam giác BHC,bằng bán kính đường tròn ngoại tiếp ABC
Cho tam giác ABC nhọn nội tiếp đường tròn O, có các đường cao AK,BI cắt nhau ở H.
a) Xác định tâm F của đường tròn ngoại tiếp tam giác BKI, tâm D của đường tròn ngoại tiếp tam giác IHF, tâm E của đường tròn ngoại tiếp tam giác AFC.
b)Cm: AEDF là hình bình hành.
Cho tam giác ABC có A=75 , C=45 và AC=a\(\sqrt{2}\) . Vẽ đường cao AK
a, Tính AB , KC theo a
b, Gọi H là trực tâm của tam giác ABC và O là tâm đường tròn ngoại tiếp tam giác ABC . Tính OHC
c, Gọi I là tâm đt nội tiếp tam giác ABC . Tính bán kính đt ngoại tiếp tam giác HOT theo a
cho tam giác ABC có ba góc nhọn . các đường cao AD,BE,CF của tam giác ABC cắt nhau tại H
a) Chứng minh CEHD nội tiếp trong một đường tròn . xác định vị trí tâm O của đường tròn ngoại tiếp tứ giác CEHD
b) chứng minh góc FEH= góc DEH
Chứng minh H là tâm đường tròn nội tiếp tam giác DEF
c)cho CH= 4cm. Tính độ dài đường tròn (O) và diện tích hình tròn (O)
Cho tam giác ABC có trực tâm H, trọng tâm G và O là tâm đường tròn ngoại tiếp. Chứng minh H, O, G thẳng hàng
Cho tam giác ABC có trực tâm H , trọng tâm G , O là tâm đường tròn
ngoại tiếp , I là trung điểm BC , AD là đường kính của (O) .
Chứng minh H , G , O thẳng hàng ?
Giải :
Ta có : góc DCA = góc DBA = 90 độ ( góc nội tiếp chắn 1/2 (O))
Xét tứ giác BHCD ta có :
BH // DC ( vì cùng vuông góc với AC )
CH // DB ( vì cùng vuông góc với AB )
Do đó tứ giác BHCD là hình bình hành .
===> H , I , D thẳng hàng và IH = ID (t/c đường chéo hbhành)
Ta lại có : OI = 1/2 AH ( đ.trung bình tam giác DAH ) (1)
GI = 1/2 GA (t/chất trọng tâm của ABC ) (2)
góc HAG = góc GIO ( so le trong vì AH // OI ) (3)
Do đó tam giác GAH đồng dạng tam giác GIO ( c.g.c)
===> góc HGA = góc IGO (góc tương ứng của 2 t.giác đ.dạng )
Vì góc HGA và góc IGO là 2 góc ở vị trí đối đỉnh bằng nhau nên ta suy ra H , G , O thẳng hàng .
Vậy trong 1 tam giác trực tâm , trọng tâm , tâm đường tròn ngoại tiếp cùng nằm trên 1 đường thẳng đó là đường thẳng Euler !
Cho I, O lần lượt là tâm đường tròn nội tiếp, ngoại tiếp của tam giác ABC với A ^ = 60 0 . Gọi H là trực tâm của ∆ABC. Chứng minh các điểm B, C, O, H, I cùng thuộc một đường tròn
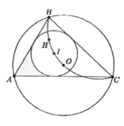
Chứng minh được B I C ^ = 120 0
=> B O C ^ = 2 B A C ^ = 120 0 => B H C ^ = 180 0 - 60 0 = 120 0 (góc nội tiếp và góc ở tâm)
=> H, I, O cùng nhìn BC dưới góc 120 0 nên B, C, O, I, H cùng thuộc một đường tròn
cho tam giác ABC nhọn, H là trực tâm nội tiếp đường tròn tâm O. Gọi H' là điểm đối xứng của H qua BC. Chứng minh
a) Tứ giác ABH'C nội tiếp
b) Bán kính đường tròn ngoại tiếp tam giác BHC bằng bán kính đường tròn ngoại tiếp tam giác ABC
MÌNH ĐANG CẦN GẤP XIN HÃY GIẢI GIÚP MÌNH SỚM NHÉ
a . Gọi AH ∩ BC=D,BH ∩ AC=E,CH ∩ AB=F
\(\Rightarrow AD\perp BC,BE\perp AC,CF\perp AB\)
\(\Rightarrow\widehat{ADC}=\widehat{AFC}=90^0\) => ◊AFDC nội tiếp
\(\Rightarrow\widehat{DCF}=\widehat{DAF}\)
VÌ H đối xứng H' qua BC
\(\Rightarrow HH'\perp BC\Rightarrow A,H,,D,H'\)thẳng hàng
\(\Rightarrow\widehat{BAH'}=\widehat{DAF}=\widehat{FDC}=\widehat{HCB}\)
Lại có: H đối xứng với H' qua BC
\(\Rightarrow\widehat{BCH'}=\widehat{HCB}\)
\(\Rightarrow\widehat{BCH'}=\widehat{BAH'}\Rightarrow\)
\(\Rightarrow BC\perp AA'\Rightarrow A,H,D,H',A'\) thẳng hàng
Vì \(H,H'\) đối xứng qua BC , A,A' đối xứng qua BC
\(\Rightarrow\widehat{BHC}=\widehat{BH'C},\widehat{BAC}=\widehat{BA'C}\)
Lại có ◊ ABH'C nội tiếp
\(\Rightarrow\widehat{BAC}+\widehat{BH'C}=180^0\)
\(\Rightarrow\widehat{BA'C}+\widehat{BHC}=180^0\)
=> ◊ BHCA' nội tiếp
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp \(\Delta A'BC\)
Ta có : A , A' đối cứng qua BC
\(\Rightarrow A'B=AB,CA=CA'\Rightarrow\Delta ABC=\Delta A'BC\left(c.c.c\right)\)
=> Bán kính đường tròn ngoại tiếp \(\Delta A'BC\) bằng bán kính đường tròn ngoại tiếp ΔABC
=> Bán kính đường tròn ngoại tiếp \(\Delta BHC\) bằng bán kính đường tròn ngoại tiếp ΔABC
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn O bán kính R.Vẽ hai đường kính AD và BE cả đường tròn , gọi h là trực tâm của tam giác ABC, . Tính diệntích hình tròn ngoại tiếp tam giác BHC theo R
giúp tớ với
Cho tam giác nhọn ABC, trực tâm H, nội tiếp đường tròn (O). Gọi H' là điểm đối xứng của H qua BC. Chứng minh:
a) Tứ giác ABH'C là tứ giác nội tiếp
b) Bán kính đường tròn ngoại tiếp tam giác BHC bằng bán kính đường tròn ngoại tiếp tam giác ABC
c) OA \(\perp\) B'C'