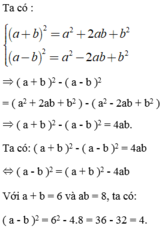Chứng minh rằng: ( a + b ) 2 - ( a - b ) 2 = 4 a b . Từ đó tính: ( a + b ) 2 biết a - b = 3 và ab = 4.
PB
Những câu hỏi liên quan
Cho a/b=b/c. Chứng minh rằng:
a^2+b^2/b^2+c^2=a/c (giải dài tí nha. hi hi!!)
Ta có:\(\frac{a}{b}=\frac{b}{c}=>\frac{a}{b}.\frac{b}{c}=\frac{a}{b}.\frac{a}{b}=>\frac{a.b}{b.c}=\frac{a^2}{b^2}=>\frac{a}{c}=\frac{a^2}{b^2}\)
\(\frac{a}{b}=\frac{b}{c}=>\frac{a}{b}.\frac{b}{c}=\frac{b}{c}.\frac{b}{c}=>\frac{a.b}{b.c}=\frac{b^2}{c^2}=>\frac{a}{c}=\frac{b^2}{c^2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{c}=\frac{a^2}{b^2}=\frac{b^2}{c^2}=\frac{a^2+b^2}{b^2+c^2}\)
=>\(\frac{a}{c}=\frac{a^2+b^2}{b^2+c^2}\)
Đúng 0
Bình luận (0)
a/b+c + b/c+a + c/a+b =1 . Chứng minh rằng a^2/b+c + b^2/c+a + c^2/a+b =0
mọi người giúp tí nha
Chứng minh rằng: ( a + b ) 2 - ( a - b ) 2 = 4 a b . Từ đó tính: ( a + b ) 2 biết a + b = 6 và ab = 8
1. Chứng minh các đẳng thức :
a) (x + y)^2 - y^2 = x(x + 2y)
b) (x^2 + y^2) - (2xy)^2 = (x + y)^2 . (x - y)^2
c) (x + y)^3 = x(x - 3y)^2 + y(y - 3x)^2
2.Chứng minh rằng :
a) (a + b)^3 + (a - b)^3 = 2a(a^2 + 3b^2)
b) (a + b)^3 - (a - b)^3 = 2b(b^2 + 3a^2)
GIÚP MK VS Ạ!!!!!!! MK VIẾT HƠI KHÓ ĐỌC TÍ
Bài 1:
a) \(\left(x+y\right)^2-y^2=x^2+2xy+y^2-y^2=x^2+2xy=x\left(x+2y\right)\)
b) Sửa đề: \(\left(x^2+y^2\right)^2-\left(2xy\right)^2=\left(x^2-2xy+y^2\right)\left(x^2+2xy+y^2\right)\)
\(=\left(x-y\right)^2\left(x+y\right)^2\)
c) \(x\left(x-3y\right)^2+y\left(y-3x\right)^2=x\left(x^2-6xy+9y^2\right)+y\left(y^2-6xy+9x^2\right)\)
\(=x^3-6x^2y+9xy^2+y^3-6xy^2+9x^2y\)
\(=x^3+3x^2y+3xy^2+y^3=\left(x+y\right)^3\)
Bài 2:
a) \(\left(a+b\right)^3+\left(a-b\right)^3=\left(a+b+a-b\right)\left[\left(a+b\right)^2-\left(a+b\right)\left(a-b\right)+\left(a-b\right)^2\right]\)
\(=2a\left(a^2+2ab+b^2-a^2+b^2+a^2-2ab+b^2\right)\)
\(=2a\left(a^2+3b^2\right)\)
b) \(\left(a+b\right)^3-\left(a-b\right)^3=\left(a+b-a+b\right)\left[\left(a+b\right)^2+\left(a+b\right)\left(a-b\right)+\left(a-b\right)^2\right]\)
\(=2b\left(a^2+2ab+b^2+a^2-b^2+a^2-2ab+b^2\right)\)
\(=2b\left(b^2+3a^2\right)\)
a, \(\left(x+y\right)^2-y^2=x\left(x+2y\right)\Leftrightarrow x^2+2xy+y^2-y^2=x^2+2xy\)
\(\Leftrightarrow x^2+2xy=x^2+2xy\left(đpcm\right)\)
b, \(\left(x^2+y^2\right)-\left(2xy\right)^2=\left(x+y\right)^2\left(x-y\right)^2\)
\(\Leftrightarrow x^2+y^2-4x^2y^2=\left(x^2+2xy+y^2\right)\left(x^2-2xy+y^2\right)\)
\(\Leftrightarrow x^2+y^2-4x^2y^2=x^4-2x^2y^2+y^4\)đề sai ?
Chứng Minh Rằng
a. cho biểu thức A= 3 + 3^2+ 3^3+ 3^4+...+ 3^100 và B= 3^100-1.Chứng Minh rằng : A<B
b. Cho A= 1+4+4^2+...+4^99, B= 4^100. Chứng Minh Rằng : A<B/3
\(A=3+3^2+3^3+...+3^{100}\)
\(\Leftrightarrow3A=3^2+3^3+3^4+3^5+....+3^{101}\)
\(\Leftrightarrow3A-A=\left(3^2+3^3+3^4+3^5+...+3^{101}\right)-\left(3+3^2+3^3+3^4+...+3^{100}\right)\)
\(\Leftrightarrow2A=3^{101}-3\)
\(\Leftrightarrow A=\frac{3^{101}-3}{2}< 3^{100}-1\)
\(\Leftrightarrow A< B\)
a. tính A = 3+3^2+3^3+3^4+.....+3^100
3A=3^2+3^3+3^4+3^5+....+3^100
3A-A=(3^2+3^3+3^4+....+3^101)-(3+3^2+3^3+3^4+.....+3^100)=3^101-3=3^100
mà B=3^100-1 => A<B
\(A=1+4+4^2+...+4^{99}\)
\(\Leftrightarrow4A=4+4^2+4^3+...+4^{100}\)
\(\Leftrightarrow3A=4^{100}-1\)
\(\Leftrightarrow A=\frac{4^{100}-1}{3}< \frac{4^{100}}{3}\)
hay A<B (đpcm)
1)chứng minh rằng nếu a+b+c=1 thì a^4 +c^4 +b^4 =abc
2) với a,b,c dương chứng minh rằng 2căna +2cănb+2cănc +a^2+b^2+c^2 >= 3(a+b+c)
mk chẳng biết nguyen hoang phi hung ak
Đúng 0
Bình luận (0)
Câu 1. Hãy viết một số hữu tỉ và một số vô tỉ lớn hơn √2 nhưng nhỏ hơn √3
Câu 2. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 3. Chứng minh rằng: [x] + [y] ≤ [x + y].
ờm,bài này ai làm dc tôi làm ny người đó luôn(đùa tí cho vui)
dễ mà,nhưng là toán lp 9 nhé
chưa từng nhìn
botay'
huhi
Đúng 0
Bình luận (0)
câu 1:
số hữu tỉ đó là: 1,659842
số vô tỉ đó là: 1,58281134........
Đúng 0
Bình luận (0)
dễ mà
tôi chỉ thử để xem ai giỏi thì kb thôi
mà bài này tôi lấy trên mạng ấy mà
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 =0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| < |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)2 0Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| |a + b|Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|Bài 8. Chứng minh rằng: |x − 1| + |x − 2| 1Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| 2Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| 4Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| 2
Đọc tiếp
Bài 5. Tìm các số thực x, y, z thỏa mãn: |x − 1| + |y − 2| + (z − x)
2 = 0
Bài 6. Với mọi số thực a, b. Chứng minh rằng: |a| + |b| > |a + b|
Bài 7. Với mọi số thực a, b. Chứng minh rằng: |a| − |b| 6 |a − b|
Bài 8. Chứng minh rằng: |x − 1| + |x − 2| > 1
Bài 9. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| > 2
Bài 10. Chứng minh rằng: |x − 1| + |x − 2| + |x − 3| + |x − 4| > 4
Bài 11. Chứng minh rằng |x − 1| + 2|x − 2| + |x − 3| > 2