Cho mặt phẳng α : 2 x + y + 2 z + 3 = 0 và điểm M(1;2;1). Khoảng cách từ điểm M đến mặt phẳng (α) bằng
A. 5
B. 3
C. 7
D. 9
PB
Những câu hỏi liên quan
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
M’ đối xứng với M qua (α)
⇒ H là trung điểm MM’
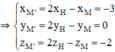
⇒ M’(-3; 0; -2).
Đúng 0
Bình luận (0)
Cho mặt cầu
(
S
)
:
(
x
+
1
)
2
+
(
y
-
2
)
2
+
(
z
-
3
)
2
25
và mặt phẳng (
α
): 2x+y-2z+m0. Các giá trị của m để (
α
) và (S) không có điểm chung là: A.
m
≤
-...
Đọc tiếp
Cho mặt cầu ( S ) : ( x + 1 ) 2 + ( y - 2 ) 2 + ( z - 3 ) 2 = 25 và mặt phẳng ( α ): 2x+y-2z+m=0. Các giá trị của m để ( α ) và (S) không có điểm chung là:
A. m ≤ - 9 hoặc m ≥ 21
B. m < - 9 hoặc m > 21
C. - 9 ≤ m ≤ 21
D. - 9 < m < 21
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0 Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α).
Đường thẳng MH vuông góc với (α)
⇒ MH nhận vtpt của (α)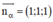 
là 1 vtcp
Mà M(1; 4; 2) ∈ MH
⇒ Pt đường thẳng MH: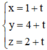 
⇒ H(1 + t; 4 + t; 2 + t).
H ∈ (α) ⇒ 1 + t + 4 + t + 2 + t – 1 = 0 ⇔ t = -2.
⇒ H(-1; 2; 0).
Đúng 0
Bình luận (0)
Cho điểm M(1; 4; 2) và mặt phẳng (α): x + y + z – 1 = 0. Tính khoảng cách từ M đến mp(α).
Khoảng cách từ M đến mặt phẳng (α) là:
Đúng 0
Bình luận (0)
Cho điểm M(1;4;2) và mặt phẳng
α
: x+y+z-10. Tìm khoảng cách từ điểm M đến mặt phẳng
α
Đọc tiếp
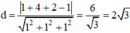
Cho điểm M(1;4;2) và mặt phẳng α : x+y+z-1=0. Tìm khoảng cách từ điểm M đến mặt phẳng α
Cho điểm M(3;-1;-2) và mặt phẳng
α
: 3x-y+z+40. Phương trình nào sau đây là phương trình mặt phẳng đi qua M và song song với
α
Đọc tiếp
Cho điểm M(3;-1;-2) và mặt phẳng α : 3x-y+z+4=0. Phương trình nào sau đây là phương trình mặt phẳng đi qua M và song song với α
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng
α
: x+y+z-40 và mặt cầu (S):
x
-
3
2
+
(
y
-
3
)
2
+
(
z
-...
Đọc tiếp
Trong không gian Oxyz cho điểm M(2;1;1) mặt phẳng α : x+y+z-4=0 và mặt cầu (S): x - 3 2 + ( y - 3 ) 2 + ( z - 4 ) 2 = 16 Phương trình đường thẳng α đi qua M và nằm trong α cắt mặt cầu (S) theo một đoạn thẳng có độ dài nhỏ nhất. Đường thẳng α đi qua điểm nào trong các điểm sau đây?
Trong không gian Oxyz, cho điểm
A
(
0
;
1
;
2
)
, mặt phẳng
α
:
x
-
y
+
z
-
4
0
và mặt cầu
S
:
(
x
-
3...
Đọc tiếp
Trong không gian Oxyz, cho điểm A ( 0 ; 1 ; 2 ) , mặt phẳng α : x - y + z - 4 = 0 và mặt cầu S : ( x - 3 ) 2 + ( y - 1 ) 2 + ( z - 2 ) 2 = 16 . Gọi (P) là mặt phẳng đi qua A, vuông góc với α và đồng thời (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính nhỏ nhất. Tọa độ giao điểm M của (P) và trục x'Ox là:
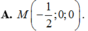
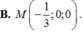
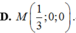
Cho điểm M(1 ; 4 ; 2) và mặt phẳng (α): x + y + z -1 = 0.
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α) ;
b) Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α).
a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .
Đúng 0
Bình luận (0)
Cho điểm M(1 ; 4 ; 2) và mặt phẳng (α): x + y + z -1 = 0.
a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α) ;
b) Tìm tọa độ điểm M' đối xứng với M qua mặt phẳng (α).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α).
a) Xét đường thẳng d qua M và d ⊥ (α).
Khi đó H chính là giao điểm của d và (α).
Vectơ (1 ; 1 ; 1) là vectơ pháp tuyến của (α) nên
là vectơ chỉ phương của d.
Phương trình tham số của đường thẳng d có dạng: .
Thay tọa độ x ; y ; z của phương trình trên vào phương trình xác định (α), ta có:
3t + 6 = 0 => t = -2 => H(-1 ; 2 ; 0).
b) Gọi M'(x ; y ; z) là điểm đối xứng của M qua mặt phẳng (α), thì hình chiếu vuông góc H của M xuống (α) chính là trung điểm của MM'.
Ta có:
=> x = -3 ;
=> y = 0 ;
=> z = -2.
Vậy M'(-3 ; 0 ;2).
c) Tính khoảng cách từ điểm M đến mặt phẳng (α) bằng 2 cách sau:
Cách 1: Áp dụng công thức ta có:
.
Cách 2: Khoảng cách từ M đến (α) chính là khoảng cách MH:
d(M,(α) )= MH = .
Đúng 0
Bình luận (0)