Số x = 1 là nghiệm của bất phương trình 2 m - 3 m x 2 ≥ 1 khi và chỉ khi
A. m ≤ - 1
B. m ≥ - 1
C. - 1 ≤ m ≤ 1
D. m ≥ - 1
Cho bất phương trình: m x 2 + 2 ( m - 1 ) x + m + 2 < 0 . Điều kiện của tham số m để bất phương trình đã cho vô nghiệm là
A. m > 0
B. m ≤ 0
C. m ≥ 1 4
D. m ≤ 1 4
+ Khi m = 0, bất phương trình trở thành - 2 x + 2 < 0 ⇔ x > 1 . Vậy m = 0 không thỏa mãn yêu cầu của bài toán.
+ Khi m ≠ 0 , bất phương trình vô nghiệm khi m x 2 + 2 m - 1 x + m + 2 ≥ 0 , ∀ x ∈ ℝ . ⇔ a > 0 ∆ ' ≤ 0 ⇔ m > 0 ( m - 1 ) 2 - m ( m + 2 ) ≤ 0 .
⇔ m > 0 - 4 m + 1 ≤ 0 ⇔ m > 0 m ≥ 1 4 ⇔ m ≥ 1 4
Chọn C.
Hệ bất phương trình 2 x - 1 > 0 x - m < 2 có nghiệm khi và chỉ khi
A. m < - 3 2
B. m ≤ - 3 2
C. m > - 3 2
D. m ≥ - 3 2
Ta có: 2 x - 1 > 0 x - m < 2 ⇔ x > 1 2 x < 2 + m
Để hệ bất phương trình có nghiệm khi và chỉ khi 1 2 < 2 + m ⇔ m > - 3 2
Cho bất phương trình : 1 - x ( m x - 2 ) < 0 ( * ) Xét các mệnh đề sau:
(1) Bất phương trình tương đương với mx - 2 <0
(2) m ≥ 0 là điều kiện cần để mọi x< 1 là nghiệm của bất phương trình (*)
(3) Với m < 0 , tập nghiệm của bất phương trình là 2/m< x< 1
Mệnh đề nào đúng?
A. Chỉ (1)
B. Chỉ (3)
C. (2) và (3)
D. Tất cả đúng
Cho bất phương trình : 1 - x ( mx - 2 ) < 0 ( * )
Xét các mệnh đề sau:
(I) Bất phương trình tương đương với mx - 2 < 0;
(II) m ≥ 0 là điều kiện cần để mọi x < 1 là nghiệm của bất phương trình (*)
(III) Với m < 0 , tập nghiệm của bất phương trình là 2 m < x < 1
Mệnh đề nào đúng?
A. Chỉ (I)
B. Chỉ (III)
C. (II) và (III)
D. Cả (I), (II), (III)
Hệ bất phương trình 2 x + 4 < 0 m x + 1 > 0 có tập nghiệm là - ∞ ; - 2 khi và chỉ khi
A. m ≤ 0
B. m < 0
C. m > 0
D. m < - 1 2
Ta có: 2x + 4 < 0 khi x < - 2.
* Xét mx + 1 > 0 (*)
+ Nếu m = 0 thì (*) trở thành: 0x + 1 >0 (luôn đúng).
+ Nếu m > 0 thì * ⇔ m x > - 1 ⇔ x > - 1 m
Suy ra, tập nghiệm của hệ bất phương trình không thể - ∞ ; - 2
+ Nếu m < 0 thì * ⇔ m x > - 1 ⇔ x < - 1 m
Để hệ bất phương trình có tập nghiệm là - ∞ ; - 2 khi và chỉ khi :
- 1 m > - 2 ⇔ - 1 + 2 m m > 0 ⇔ - 1 + 2 m < 0 ( vì m < 0)
⇔ 2 m < 1 ⇔ m < 1 2
Kết hợp điều kiện m < 0 ta được: m < 0
Từ các trường hợp trên suy ra: m ≤ 0 .
Cho hàm số y=f(x) có bảng biến thiên như hình vẽ.
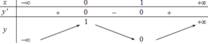
Khi đó phương trình f(x) +1=m có ba nghiệm thực phân biệt khi và chỉ khi
A. 1<m<2
B. 1 ≤ m ≤ 2
C. 0 ≤ m ≤ 1
D. 0<m<1
Cho bất phương trình x 4 + x 2 + m 3 - 2 x 2 + 1 3 + x 2 x 2 - 1 > 1 - m . Tìm tất cả các giá trị thực của tham số m để bất phương trình trên nghiệm đúng ∀ x > 1 .
![]()
![]()

![]()
Tập tất cả các giá trị của tham số m để bất phương trình m 2 + 3 m x ≤ m 2 nghiệm đúng với mọi x là:
A. (0;1)
B. {0}
C. {0;1}
D. {1}
* Nếu m= 0 thì bất phương trình đã cho trở thành:
0x < 0( luôn đúng với mọi x).
* Nếu m= 1 thì bất phương trình đã cho trở thành:
0x < 1 ( luôn đúng với mọi x)
Tập tất cả các giá trị của tham số m để bất phương trình đã cho nghiệm đúng với mọi x là {0; 1}
Tập tất cả các giá trị của tham số m để hệ bất phương trình 2 x - 1 ≥ 3 x - m ≤ 0 có nghiệm duy nhất là
A. ∅
B. 2
C. [ 2 ; + ∞ )
D. ( - ∞ ; 2 ]
Ta có 2 x - 1 ≥ 3 x - m ≤ 0 ⇔ x ≥ 2 x ≤ m . Hệ có nghiệm duy nhất khi và chỉ khi m = 2