Nghiệm của phương trình 2sin2 x- 3sin x+ 1= 0 thỏa điều kiện: 0 ≤ x < π 2
A. x = π /6
B. x = π /4
C. x = π /2
D. x = - π /2
Nghiệm của phương trình cos2 x- cosx = 0 thỏa mãn điều kiện 0 < x < π
A. x= π / 6
B. x= π / 2
C. x= π / 4
D. x=- π / 2
Hướng dẫn giải
Chọn B.
Ta có : cos2 x- cosx = 0 ó cosx. ( cosx – 1) = 0
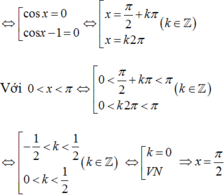
Nghiệm của phương trình sin2x – sinx = 0 thỏa điều kiện: 0 < x < π
A. x = π 2 .
B. x = π
C. x = 0
D. x = - π 2
Hướng dẫn giải
Chọn A.
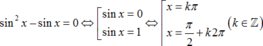
Vì 0 < x < π nên nghiệm của phương trình là x = π 2 .
Tìm nghiệm của phương trình lượng giác cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π
A. x = π 2
B. x=0
C. x= π
D. x=2
Đáp án A
Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
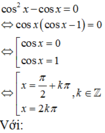
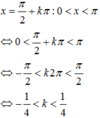
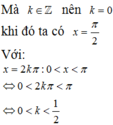
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.
Sai lầm và chú ý: Đối với những bài toán giải phương trình lượng giác thỏa mãn điều kiện cho trước, ta cần tìm được x sau đó cho x thỏa mãn điều kiện đầu bài và cô lập được k khi đó ta sẽ tìm được giá trị nguyên k thỏa mãn và sẽ tìm đc x.
Nghiệm của phương trình sin 2 x - sin x = 0 thỏa mãn điều kiện: 0 < x < π
![]()
![]()
![]()
![]()
Nghiệm của phương trình cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π là
A. x = π 2
B. x = - π 2
C. x = π 6
D. x = π 4
Tìm nghiệm của phương trình lượng giác cos 2 x − cos x = 0 thỏa mãn điều kiện 0 < x < π
A. x = π 2
B. x = 0
C. x = π
D. x = 2
Đáp án A
Phương pháp: Giải phương trình lượng giác sau đó kết hợp vào điều kiện của đầu bài để tìm ra nghiệm thỏa mãn.
Cách giải:
cos 2 x − cos x = 0
⇔ cos x cos x − 1 = 0
⇔ cos x = 0 cos x = 1
⇔ x = π 2 + k π x = 2 k π , k ∈ ℤ
+) Với: x = π 2 + k π : 0 < x < π ⇔ 0 < π 2 + k π < π ⇔ − π 2 < k 2 π < π 2 ⇔ − 1 4 < k < 1 4
Mà k ∈ ℤ nên k = 0 khi đó ta có x = π 2
+) Với: x = 2 k π : 0 < x < π ⇔ 0 < 2 k π < π ⇔ 0 < k < 1 2
Mà k ∈ ℤ nên không có giá trị k nào thỏa mãn.
Có bao nhiêu nghiệm của phương trình sin 2 x - sin x = 0 thỏa mãn điều kiện 0 < x < π
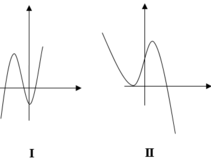
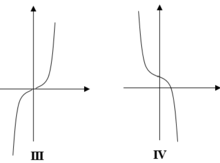
A. Đồ thị (III) xảy ra khi
B. Đồ thị (IV) xảy ra khi
C. Đồ thị (II) xảy ra khi
D. Đồ thị (I) xảy ra khi
Nghiệm của phương trình lượng giác cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π là
A. 0
B. 3 π 4
C. π 2
D. - π 2
Nghiệm của phương trình lượng giác cos 2 x - cos x = 0 thỏa mãn điều kiện 0 < x < π là
A. x = 0
B. x = 3 π 4
C. x = π 2
D. x = - π 2