Cho tứ giác ABCD là hình bình hành và B A D ⏜ = 90 0 . Tìm tâm đường tròn ngoại tiếp tứ giác ABCD?
A. Trung điểm AC
B. Điểm A
C. Điểm B
D. Điểm D
PB
Những câu hỏi liên quan
Cho hình thang ABCD đáy lớn AD đáy nhỏ BC nội tiếp đường tròn tâm O. AB và CD kéo dài cắt nhau tại I. Các tiếp tuyến của đường tròn (O) tại B và D cắt nhau tại K.a C/m tứ giác BIKD nội tiếpb C/m IK//BCc Hình thang ABCD cần thêm điều kiện gì để tứ giác AIKD là hình bình hành. Khi đó c/m hệ thức: IC.IEID.CE( với E là giao điểm của BK và ID)d Vẽ hình bình hành BDKM, đường tròn ngoại tiếp tam giác BKM cắt đường tròn (O) tại điểm thứ 2N.C/m 3 điểm D,M,N thẳng hàng.
Đọc tiếp
Cho hình thang ABCD đáy lớn AD đáy nhỏ BC nội tiếp đường tròn tâm O. AB và CD kéo dài cắt nhau tại I. Các tiếp tuyến của đường tròn (O) tại B và D cắt nhau tại K.
a> C/m tứ giác BIKD nội tiếp
b> C/m IK//BC
c> Hình thang ABCD cần thêm điều kiện gì để tứ giác AIKD là hình bình hành. Khi đó c/m hệ thức: IC.IE=ID.CE( với E là giao điểm của BK và ID)
d> Vẽ hình bình hành BDKM, đường tròn ngoại tiếp tam giác BKM cắt đường tròn (O) tại điểm thứ 2N.C/m 3 điểm D,M,N thẳng hàng.
Cho em xin đáp án câu c bài này ah
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD với góc BAD < 90 độ. Đường phân giác của góc BCD cắt đường tròn ngoại tiếp tam giác BCD tại O khác C. kẻ đường thẳng d đi qua A và vuông góc với CO. Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E và F. Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác CEF.
cho hình bình hành ABCD, góc A nhỏ hơn 900. Đường tròn ngoại tiếp của tam giác BCD cắt AC ở E. Chứng minh BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB
ta có BAC^=DCA^(ABCD là hbh")nên AB//CD(*)
xét đg tròn (O)có EBD^=ECD^(cùng chắn cug ED)=>ECD^=ACD^(E thc AD)(**)
từ (*)(**)=>BAC^=EBD^ hay BAE^+EBD^
xét BAE^laf góc nt chắn cug BE của (O')nên BAE^=1/2SĐ BC
=>EBD^=1/2sđBE
=>đfcm
Cho tam giác ABC nội tiếp (O). Một đường tròn tâm I tùy ý đi qua B và C cắt AB và AC theo thứ tự tại M và N. Đường tròn tâm K ngoại tiếp tam giác AMN cắt đường tròn (O) tại điểm thứ hai D. CMR a/ AKIO là hình bình hành ( đã làm) b/ góc ADI=90 độ
Cho hình bình hành ABCD với
B
A
D
^
90
∘
.Đường phân giác của góc
B
C
D
^
cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.Kẻ đường thẳng d đi qua A và vuông góc với CO.Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại...
Đọc tiếp
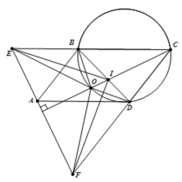
Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
2). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác △ C E F .
3). Gọi giao điểm của OC và BD là I, chứng minh rằng I B . B E . E I = I D . D F . F I .
.
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD với
B
A
D
^
90
∘
.Đường phân giác của góc
B
C
D
^
cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.Kẻ đường thẳng d đi qua A và vuông góc với CO.Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại...
Đọc tiếp
Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
2). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác △ C E F .
3). Gọi giao điểm của OC và BD là I, chứng minh rằng I B . B E . E I = I D . D F . F I .
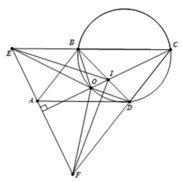
2). Từ Δ O B E = Δ O D C ⇒ O E = O C .
Mà CO là đường cao tam giác cân CEF , suy ra OE=OF.
Từ đó
O
E
=
O
C
=
O
F
, vậy O là tâm đường tròn ngoại tiếp tam giác .
Đúng 0
Bình luận (0)
Cho tam giác ABC nội tiếp (O). Một đường tròn tâm I tùy ý đi qua B và C cắt AB và AC theo thứ tự tại M và N. Đường tròn tâm K ngoại tiếp tam giác AMN cắt đường tròn (O) tại điểm thứ hai D. CMR
a/ AKIO là hình bình hành ( đã làm)
b/ góc ADI=90 độ
Mọi người làm lại ý a) giúp mình với.
Bạn tìm đc lời giải chx cho mik xin lời giải với
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD, A nhỏ hơn 90 độ. Đường tròn ngoại tiếp tam giác BCD cắt AC ở E. Chứng minh rằng BD là tiếp tuyến của đường tròn ngoại tiếp tam giác AEB
Cho hình bình hành ABCD, đường phân giác của góc
BAD^
cắt CD và BC tại M và N. Gọi O là tâm đường tròn ngoại tiếp tam giác CMN.
a) Chứng minh bốn điểm O , B , C , D nằm trên một đường tròn.