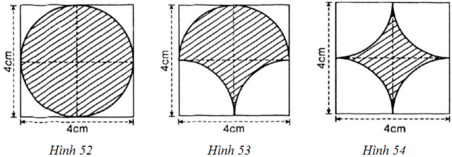
Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi mỗi hình (có gạch chéo):
PB
Những câu hỏi liên quan
Vẽ lại ba hình (tạo bởi các cung tròn) dưới đây và tính chu vi mỗi hình (có gạch chéo):
- Hình 52:
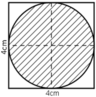
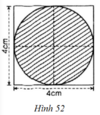
Phần gạch chéo là đường tròn đường kính d = 4cm
⇒ Chu vi của hình là: C = π.d = 4π ≈ 12,57 (cm)
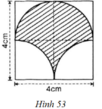
- Hình 53:
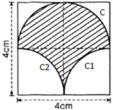
Chu vi gồm nửa đường tròn C; cung tròn C1 và cung tròn C2.
+ C là nửa đường tròn đường kính d = 4cm
⇒ C = π.d/2 = 2π (cm)
+ C1 và C2 là ¼ đường tròn bán kính R = 2cm
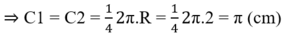
Vậy chu vi phần gạch chéo bằng:
C + C1 + C2 = 2π + π + π = 4π ≈ 12,57 (cm)
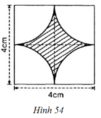
- Hình 54:
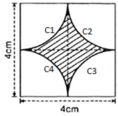
Chu vi cần tính là 4 cung tròn C1 ; C2; C3; C4.
C1 ; C2; C3; C4 đều là ¼ đường tròn bán kính R = 2cm.
⇒ C1 = C2 = C3 = C4
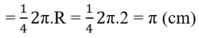
⇒ Chu vi phần hình gạch chéo:
C = C1 + C2 + C3 + C4 = 4π ≈ 12,57 (cm).
Đúng 0
Bình luận (0)
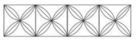
Mỗi viên gạch hoa hình vuông có cạnh 20cm.
a) Tính chu vi hình vuông ghép bởi 4 viên gạch hoa như hình vẽ dưới đây:
b) Tính chu vi hình hữ nhật ghép bởi 4 viên gạch hoa như hình vẽ dưới đây:
a) Cạnh hình vuông là: 20 + 20 = 40 (cm)
Chu vi hình vuông là 40 x 4 = 160 (cm)
b) Chiều rộng hình chữ nhật là: 20 (cm)
Chiều dài hình chữ nhật là: 20 x 4 = 80 (cm)
Chu vi hình chữ nhật là: (20 + 80) x 2 = 200 (cm)
Đúng 0
Bình luận (0)
Viết sai chính tả: hình chữ nhật mà ghi hình hữ nhật.
có viết sai đâu?Xem thêm câu trả lời
mỗi viên gạch hoa hình vuông có cạnh 20cm.a tính chu vi hình vuông ghép bởi 4 viên gạch hoa. b tính chu vi hình chữ nhật ghép bởi 4 viên gạch hoa như hình vẽ dưới đây
Xem chi tiết
bài giải
chu vi hình vuông là :
20 x 4 = 80 ( cm )
chui vi hình chữ nhật là :
( 20 + 4 ) x 2=120 ( cm )
đáp số : chu vi hình vuông : 80 cm
chu vi hình chữ nhật : 120 cm
Mỗi viên gạch hình vuông có chu vi 40 cm. Tính chu vi hình ghép bởi 3 viên gạch đó như hình vẽ dưới đây
ok
baì giải
3 viên gạch có chu vi là:
40x3=120{cm}
đáp số:120 cm
Xem thêm câu trả lời
Mỗi viên gạch hoa hình vuông có cạnh 10cm. Tính chu vi hình chữ nhật ghép bởi 4 viên gạch hoa như hình vẽ dưới đây:
9999999999999999999999999999999
đầu tiên 10 x 2 = 20 , tiếp theo 20 x 4 = 80 nha
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
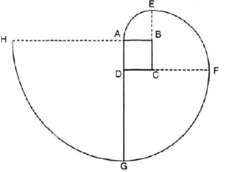
Hình 55
Cách vẽ:
Kiến thức áp dụng
+ Độ dài đường tròn đường kính d là: C = π.d
Đúng 0
Bình luận (0)
Vẽ lại hình tạo bởi các cung tròn dưới đây với tâm lần lượt là B, C, D, A theo đúng kích thước đã cho (cạnh hình vuông ABCD dài 1cm). Nêu cách vẽ đường xoắn AEFGH. Tính độ dài đường xoắn đó.
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI 10cm và HO BI 2cm. Nêu cách vẽ.b) Tính diện tích hình HOABINH (miền gạch sọc).c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .Hình 62
Đọc tiếp
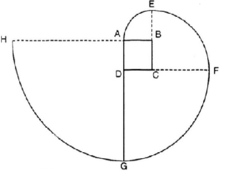
a) Vẽ hình 62 (tạo bởi các cung tròn) với HI = 10cm và HO = BI = 2cm. Nêu cách vẽ.
b) Tính diện tích hình HOABINH (miền gạch sọc).
c) Chứng tỏ rằng hình tròn đường kính NA có cùng diện tích với hình HOABINH đó .
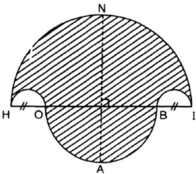
Hình 62
a) Cách vẽ
- Vẽ nửa đường tròn đường kính HI = 10cm, tâm M.
- Trên đường kính HI lấy điểm O và điểm B sao cho HO = BI = 2cm.
- Vẽ hai nửa đường tròn đường kính HO, BI nằm cùng phía với đường tròn (M).
- Vẽ nửa đường tròn đường kính OB nằm khác phía đối với đường tròn (M). Đường thẳng vuông góc với HI tại M cắt (M) tại N và cắt đường tròn đường kính OB tại A.
b)
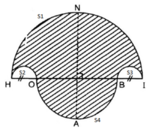
Diện tích miền gạch sọc bằng:
S = S 1 − S 2 − S 3 + S 4
với:
+ S 1 là nửa đường tròn đường kính HI
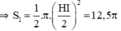
+ S 2 ; S 3 là nửa đường tròn đường kính HO và BI.
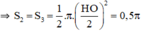
+ Ta tính OB:
Ta có: HO+ OB + BI = HI
⇔ 2+ OB + 2= 10 nên OB = 6
+ S4 là nửa đường tròn đường kính OB
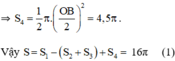
c)Ta có: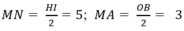 
Do đó, NA = MN+ MA= 8
Diện tích hình tròn đường kính NA bằng : π 4 2 = 16 π ( c m 2 ) ( 2 )
so sánh (1) và (2) ta thấy hình tròn đường kính NA có cùng diện tích với hình HOABINH.
Đúng 0
Bình luận (0)
Hình dưới đây được tạo bởi 3/4 hình tròn Em hãy tính chu vi hình bên dưới bán kính là 3
Hình dưới nào vậy em?
Đúng 0
Bình luận (0)